修改时间:2024-07-13 浏览次数:312 类型:中考模拟
|
3 |
2.5 |
0.6 |
1 |
2 |
2 |
2 |
3.3 |
2.5 |
1.8 |
|
2.5 |
2.2 |
3.5 |
4 |
1.5 |
2.5 |
3.1 |
2.8 |
3.3 |
2.4 |
整理数据:
|
网上学习时间x(时) |
0<x≤1 |
1<x≤2 |
2<x≤3 |
3<x≤4 |
|
人数 |
2 |
5 |
8 |
5 |
分析数据:
|
统计量 |
平均数 |
中位数 |
众数 |
|
数值 |
2.4 |
m |
n |
根据以上信息,解答下列问题:
根据图1和图2中所给信息,解答下列问题:
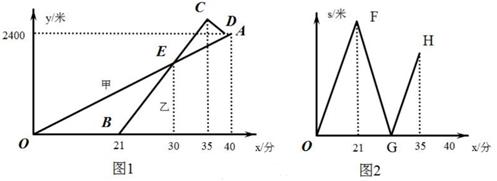
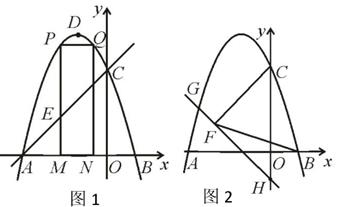
试题篮