北京市东城区2018-2019学年七年级下学期数学期末考试试卷

1. 在平面直角坐标系 xOy 中，点 P (2， -4)在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

查看解析收藏纠错

+选题
2. 若解集在数轴上的表示如图所示，则这个不等式组可以是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 正十边形的外角的度数是（）

A . 18° B . 36° C . 45° D . 60°

查看解析收藏纠错

+选题
4. 下面两个统计图反映的是甲、乙两所学校三个年级的学生在各校学生总人数中的占比情况，下列说法错误的是（）

A . 甲校中七年级学生和八年级学生人数一样多 B . 乙校中七年级学生人数最多 C . 乙校中八年级学生比九年级学生人数少 D . 甲、乙两校的九年级学生人数一样多

查看解析收藏纠错

+选题
5. 若实数a，b ， c在数轴上对应的点如图所示，则下列式子中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 若三角形两条边的长分别是 3，5，第三条边的长是整数，则第三条边的长的最大值是（）

A . 2 B . 3 C . 7 D . 8

查看解析收藏纠错

+选题
7. 不等式 x - 3≤0 的正整数解的个数是（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
8. 下列命题正确的是（）

A . 三角形的三条中线必交于三角形内一点 B . 三角形的三条高均在三角形内部 C . 三角形的外角可能等于与它不相邻的内角 D . 四边形具有稳定性

查看解析收藏纠错

+选题
9. 若多边形的内角和大于 900°，则该多边形的边数最小为（）

A . 9 B . 8 C . 7 D . 6

查看解析收藏纠错

+选题
10. 点 P(x， y) 为平面直角坐标系 xOy 内一点，xy＞0 ，且点 P 到x轴，y 轴的距离分别为 2，5，则点 P 的坐标为（）

A . (2， 5) 或(-2，-5) B . (5， 2) 或(-5，-2) C . (5， 2) 或(-2，-5) D . (2， 5) 或(-5，-2)

查看解析收藏纠错

+选题

11. $\text{[math]}$ 的算术平方根是

查看解析收藏纠错

+选题
12. 如图，△ABC 的外角平分线 AM 与边 BC 平行，则∠B∠C（填“＞”，“=”，或 “＜”）．

查看解析收藏纠错

+选题
13. 请写出一个比1大比2小的无理数：。

查看解析收藏纠错

+选题
14. 如图，在长方形 ABCD 内，两个小正方形的面积分别为 1，2，则图中阴影部分的面积等于．

查看解析收藏纠错

+选题
15. 2002 年在北京召开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的．弦图是由四个能够重合的直角三角形与一个小正方形拼成的一个大正方形（如图）．如果小正方形的面积为 1，大正方形的面积为 25，那么直角三角形斜边上的高等于．

查看解析收藏纠错

+选题
16. 在平面直角坐标系 xOy 中，对于平面内任意一点(x， y)，规定以下两种变化：
① f (x， y) = (-x， y) ．如 f (1， 2) = (-1， 2) ；

② g ( x， y) = (x， 2 - y)．

根据以上规定：

（1） g (1， 2) =（）；

（2） f (g (2， -1)) =（）

查看解析收藏纠错

+选题
17. 如图，已知等边△ABC．若以 BC 为一条边在其上方作等腰直角△BCD，则∠ABD 的度数为．

查看解析收藏纠错

+选题
18. 2019 年 4 月 27 日，第二届“一带一路”国际合作高峰论坛圆满闭幕．“一带一路”已成为我国参与全球开放合作、改善全球经济治理体系、促进全球共同发展繁荣、推动构建人类命运共同体的中国方案．其中中欧班列见证了“一带一路”互联互通的跨越式发展，年运送货物总值由 2011 年的不足 6 亿美元，发展到 2018 年的约 160 亿美元．下面是 2011-2018 年中欧班列开行数量及年增长率的统计图．
根据图中提供的信息填空：

（1） 2018 年，中欧班列开行数量的增长率是；

（2）如果 2019 年中欧班列的开行数量增长率不低于 50%，那么 2019 年中欧班列开行数量至少是列．

查看解析收藏纠错

+选题

19. 计算： $\text{[math]}$

查看解析收藏纠错

+选题
20. 下面是小明设计的“分别以两条已知线段为腰和底边上的高作等腰三角形”的尺规作图过程．
已知：线段 a， b．

求作：等腰△ABC，使线段 a 为腰，线段 b 为底边 BC 上的高．作法：如图，

①画直线 l，作直线 m⊥l，垂足为 P；

②以点 P 为圆心，线段 b 的长为半径画弧，交直线 m 于点 A；

③以点 A 为圆心，线段 a 的长为半径画弧，交直线 l 于 B，C 两点；

④分别连接 AB， AC；

所以△ABC 就是所求作的等腰三角形．根据小明设计的尺规作图过程，

（1）使用直尺和圆规，补全图形；（保留作图痕迹）

（2）完成下面的证明．
证明：∵=，

∴△ABC 为等腰三角形（填推理的依据）．

查看解析收藏纠错

+选题
21. 若一个正数的两个平方根分别为a -1， 2a + 7 ，求代数式2(a²- a +1)-(a² - 2a)+ 3 的值．

查看解析收藏纠错

+选题
22. 解不等式组 $\text{[math]}$ ，并把解集表示在数轴上．

查看解析收藏纠错

+选题
23. 在△ABC 中，∠ABC 和∠ACB 的角平分线交于点 M．

（1）若∠ABC=40°，∠ACB=60°，求∠BMC 的度数；

（2） ∠BMC 可能是直角吗？作出判断，并说明理由．

查看解析收藏纠错

+选题
24. 关于x的方程 $\text{[math]}$ 的解是负数，求字母k的值．

查看解析收藏纠错

+选题
25. 镇政府想了解李家庄 130 户家庭的经济情况，从中随机抽取了部分家庭进行调查，获得了他们的年收入（单位：万元），并对数据（年收入）进行整理、描述和分析．下面给出了部分信息．
a．被抽取的部分家庭年收入的频数分布直方图和扇形统计图如下（数据分组：0.9≤x＜1.3，1.3≤x＜1.7 ， 1.7≤x＜2.1， 2.1≤x＜2.5， 2.5≤x＜2.9 ， 2.9≤x＜3.3 ）

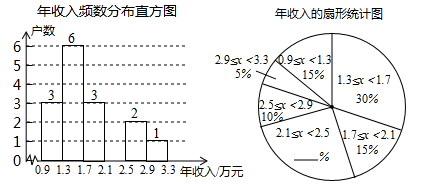
b．家庭年收入在1.3≤x＜1.7 这一组的是： 1.3 1.3 1.4 1.5 1.6 1.6

根据以上信息，完成下列问题：

（1）将两个统计图补充完整；

（2）估计李家庄有多少户家庭年收入不低于 1.5 万元且不足 2.1 万元？

查看解析收藏纠错

+选题
26. 如图，四边形 ABCD 中，AE，DF 分别是∠BAD，∠ADC 的平分线，且 AE⊥DF 于点 O ．延长 DF 交 AB 的延长线于点 M ．

（1）求证：AB∥DC ；

（2）若∠MBC=120°，∠BAD=108°，求∠C，∠DFE 的度数．

查看解析收藏纠错

+选题
27. 在平面直角坐标系 xOy 中，点A，B的坐标分别为（-2，0），（1，0）．同时将点A ，B先向左平移1个单位长度，再向上平移2个单位长度，得到点A，B的对应点依次为C，D，连接CD，AC， BD ．

（1）写出点C ， D 的坐标；

（2）在 y 轴上是否存在点E，连接EA ，EB，使S_△EAB=S_{四边形ABDC}？若存在，求出点E的坐标；若不存在，说明理由；

（3）点 P 是线段 AC 上的一个动点，连接 BP ， DP ，当点 P 在线段 AC 上移动时（不与 A ， C 重合），直接写出∠CDP 、∠ABP 与∠BPD 之间的等量关系．

查看解析收藏纠错

+选题
28. 对于任意一点 P 和线段 a．若过点 P 向线段 a 所在直线作垂线，若垂足落在线段 a 上，则称点 P 为线段a 的内垂点．在平面直角坐标系 xOy 中，已知点 A(-1，0)，B(2，0 ) ，C(0，2)．

（1）在点 M（1，0），N（3，2），P（-1，-3）中，是线段 AB 的内垂点的是；

（2）已知点 D（-3，2），E（-3，4）．在图中画出区域并用阴影表示，使区域内的每个点均为 Rt△CDE三边的内垂点；

（3）已知直线 m 与 x 轴交于点 B，与 y 轴交于点 C，将直线 m 沿 y 轴平移 3 个单位长度得到直线 n ．若存在点 Q，使线段 BQ 的内垂点形成的区域恰好是直线 m 和 n 之间的区域（包括边界），直接写出点 Q 的坐标．

查看解析收藏纠错

+选题

北京市东城区2018-2019学年七年级下学期数学期末考试试卷

一、选择题

二、填空题

三、综合题

相关试卷收起∨

北京市东城区2018-2019学年七年级下学期数学期末考试试卷

一、选择题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨