2017年浙江中考真题分类汇编（数学）：专题10 四边形

修改时间：2017-12-25 浏览次数：2995 类型：二轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1.
如图，矩形纸片ABCD中，AB=4，BC=6，将△ABC沿AC折叠，使点B落在点E处，CE交AD于点F，则DF的长等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2.
四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为S的小正方形EFGH．已知AM为Rt△ABM较长直角边，AM=2 $\text{[math]}$ EF，则正方形ABCD的面积为（）

A . 12S B . 10S C . 9S D . 8S

查看解析收藏纠错

+选题
3.
在探索“尺规三等分角”这个数学名题的过程中，曾利用了如图，该图中，四边形ABCD是矩形，E是BA延长线上一点，F是CE上一点，∠ACF=∠AFC，∠FAE=∠FEA。若∠ACB=21°，则∠ECD的度数是（）

A . 7° B . 21° C . 23° D . 24°

查看解析收藏纠错

+选题
4.
一张矩形纸片 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，小明按所给图步骤折叠纸片，则线段 $\text{[math]}$ 长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5.
如图，在平面直角坐标系 $\text{[math]}$ 中，已知点 $\text{[math]}$ ， $\text{[math]}$ ．若平移点 $\text{[math]}$ 到点 $\text{[math]}$ ，使以点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是菱形，则正确的平移方法是（）

A . 向左平移1个单位，再向下平移1个单位 B . 向左平移 $\text{[math]}$ 个单位，再向上平移1个单位 C . 向右平移 $\text{[math]}$ 个单位，再向上平移1个单位 D . 向右平移1个单位，再向上平移1个单位

查看解析收藏纠错

+选题
6.
如图，在▱ABCD中，连结AC，∠ABC=∠CAD=45°，AB=2，则BC的长是（）

A . $\text{[math]}$ B . 2 C . 2 $\text{[math]}$ D . 4

查看解析收藏纠错

+选题
7.
如图，四边形ABCD是边长为6的正方形，点E在边AB上，BE＝4，过点E作EF∥BC，分别交BD、CD于G、F两点．若M、N分别是DG、CE的中点，则MN的长为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 4

查看解析收藏纠错

+选题
8.
如图，矩形EFGH四个顶点分别在菱形ABCD的四条边上，BE=BF，将△AEH，△CFG分别沿边EH，FG折叠，当重叠部分为菱形且面积是菱形ABCD面积的 $\text{[math]}$ 时，则 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 4

查看解析收藏纠错

+选题

二、填空题

9.
如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B在第一象限，点D在边BC上，且∠AOD=30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，B′和B分别对应）．若AB=1，反比例函数y= $\text{[math]}$ （k≠0）的图象恰好经过点A′，B，则k的值为．

查看解析收藏纠错

+选题
10.
如图为某城市部分街道示意图，四边形ABCD为正方形，点G在对角线BD上，GE⊥CD，GF⊥BC，AD=1500m，小敏行走的路线为B→A→G→E，小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m，则小聪行走的路程为m.

查看解析收藏纠错

+选题
11.
我国三国时期数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”，如图1所示.在图2中，若正方形ABCD的边长为14，正方形IJKL的边长为2，且IJ//AB，则正方形EFGH的边长为.

查看解析收藏纠错

+选题
12.
如图，在菱形纸片ABCD中，AB＝2，∠A＝60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F、G分别在边AB、AD上．则cos∠EFG的值为．

查看解析收藏纠错

+选题
13.
如图，有一个不定的正方形ABCD，它的两个相对的顶点A，C分别在边长为1的正六边形一组对边上，另外两个顶点B，D在正六边形内部（包括边界），则正方形边长a的取值范围是

查看解析收藏纠错

+选题
14.
在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S（m²）.
①如图1，若BC＝4m，则S＝m.
②如图2，现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其它条件不变.则在BC的变化过程中，当S取得最小值时，边BC的长为m.

查看解析收藏纠错

+选题

三、解答题

15.
如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC于点E，GF⊥BC于点F，连结AG．

（1）写出线段AG，GE，GF长度之间的数量关系，并说明理由；

（2）若正方形ABCD的边长为1，∠AGF=105°，求线段BG的长．

查看解析收藏纠错

+选题
16.
如图， $\text{[math]}$ 是 $\text{[math]}$ 的中线， $\text{[math]}$ 是线段 $\text{[math]}$ 上一点（不与点 $\text{[math]}$ 重合）． $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，连结 $\text{[math]}$ ．

（1）如图1，当点 $\text{[math]}$ 与 $\text{[math]}$ 重合时，求证：四边形 $\text{[math]}$ 是平行四边形；

（2）如图2，当点 $\text{[math]}$ 不与 $\text{[math]}$ 重合时，（1）中的结论还成立吗？请说明理由.

（3）如图3，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，且 $\text{[math]}$ ．当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
17.
在一次课题学习中，老师让同学们合作编题．某学习小组受赵爽弦图的启发，编写了下面这道题，请你来解一解．
如图，将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H，使得AE＝CG，BF＝DH，连结EF、FG、GH、HE．

（1）求证：四边形EFGH为平行四边形；

（2）若矩形ABCD是边长为1的正方形，且∠FEB＝45°，tan∠AEH＝2，求AE的长．

查看解析收藏纠错

+选题
18.
如图，在矩形ABCD中，点E是AD上的一个动点，连接BE，作点A关于BE的对称点F，且点F落在矩形ABCD的内部，连结AF，BF，EF，过点F作GF⊥AF交AD于点G，设 $\text{[math]}$ =n.

（1）求证：AE=GE；

（2）当点F落在AC上时，用含n的代数式表示 $\text{[math]}$ 的值；

（3）若AD=4AB，且以点F，C，G为顶点的三角形是直角三角形，求n的值.

查看解析收藏纠错

+选题
19.
小黄准备给长8m，宽6m的长方形客厅铺设瓷砖，现将其划分成一个长方形ABCD区域Ⅰ（阴影部分）和一个环形区域Ⅱ（空白部分），其中区域Ⅰ用甲、乙、丙三种瓷砖铺设，且满足PQ∥AD，如图所示．

（1）若区域Ⅰ的三种瓷砖均价为300元/m² ，面积为S（m²），区域Ⅱ的瓷砖均价为200元/m² ，且两区域的瓷砖总价为不超过12000元，求S的最大值；

（2）若区域Ⅰ满足AB：BC=2：3，区域Ⅱ四周宽度相等
①求AB，BC的长；
②若甲、丙两瓷砖单价之和为300元/m² ，乙、丙瓷砖单价之比为5：3，且区域Ⅰ的三种瓷砖总价为4800元，求丙瓷砖单价的取值范围．

查看解析收藏纠错

+选题
20.
如图，在△ABC中，AC=BC，∠ACB=90°，⊙O（圆心O在△ABC内部）经过B、C两点，交AB于点E，过点E作⊙O的切线交AC于点F．延长CO交AB于点G，作ED∥AC交CG于点D

（1）求证：四边形CDEF是平行四边形；

（2）若BC=3，tan∠DEF=2，求BG的值．

查看解析收藏纠错

+选题
21.
如图1，已知▱ABCD，AB//x轴，AB=6，点A的坐标为（1，-4），点D的坐标为（-3，4），点B在第四象限，点P是▱ABCD边上的一个动点.

（1）若点P在边BC上，PD=CD，求点P的坐标.

（2）若点P在边AB，AD上，点P关于坐标轴对称的点Q落在直线y=x-1上，求点P的坐标.

（3）若点P在边AB，AD，CD上，点G是AD与y轴的交点，如图2，过点P作y轴的平行线PM，过点G作x轴的平行线GM，它们相交于点M，将△PGM沿直线PG翻折，当点M的对应点落在坐标轴上时，求点P的坐标（直接写出答案）.

查看解析收藏纠错

+选题
22.
定义：有一组邻边相等，并且它们的夹角是直角的凸四边形叫做等腰直角四边形.

（1）如图1，等腰直角四边形ABCD，AB=BC，∠ABC=90°，
①若AB=CD=1，AB//CD，求对角线BD的长.
②若AC⊥BD，求证：AD=CD.

（2）如图2，在矩形ABCD中，AB=5，BC=9，点P是对角线BD上一点，且BP=2PD，过点P作直线分别交边AD，BC于点E，F，使四边形ABFE是等腰直角四边形.求AE的长.

查看解析收藏纠错

+选题
23.
在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC，连结OB，D为OB的中点。点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF。已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒。

（1）如图1，当t=3时，求DF的长；

（2）如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值；

（3）连结AD，当AD将△DEF分成的两部分面积之比为1：2时，求相应t的值。

查看解析收藏纠错

+选题
24.
如图1，在平面直角坐标系中，四边形OABC各顶点的坐标分别O(0，0)，A(3，3 $\text{[math]}$ )，B(9，5 $\text{[math]}$ )，C(14，0).动点P与Q同时从O点出发，运动时间为t秒，点P沿OC方向以1单位长度/秒的速度向点C运动，点Q沿折线OA−AB−BC运动，在OA，AB，BC上运动的速度分别为3， $\text{[math]}$ ， $\text{[math]}$ (单位长度/秒)﹒当P，Q中的一点到达C点时，两点同时停止运动．

（1）求AB所在直线的函数表达式.

（2）如图2，当点Q在AB上运动时，求△CPQ的面积S关于t的函数表达式及S的最大值.

（3）在P，Q的运动过程中，若线段PQ的垂直平分线经过四边形OABC的顶点，求相应的t值.

查看解析收藏纠错

+选题
25.
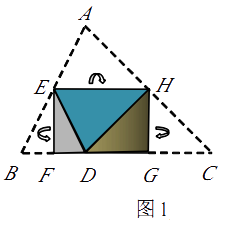
如图1，将△ABC纸片沿中位线EH折叠，使点A的对称点D落在BC边上，再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF，HG折叠，折叠后的三个三角形拼合形成一个矩形.类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形.

（1）将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG，则操作形成的折痕分别是线段，；S矩形AEFG：S□ABCD=

（2） ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH，若EF=5，EH=12，求AD的长.

（3）如图4，四边形ABCD纸片满足AD∥BC，AD<BC，AB⊥BC，AB=8，CD=10.小明把该纸片折叠，得到叠合正方形.请你帮助画出叠合正方形的示意图，并求出AD，BC的长.

查看解析收藏纠错

+选题

2017年浙江中考真题分类汇编（数学）：专题10 四边形

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨