初中数学华师大版九年级上学期第23章 23.3.3 相似三角形的性质

修改时间：2019-10-16 浏览次数：186 类型：单元试卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 下列命题是真命题的是（）

A . 如果两个三角形相似，相似比为4:9，那么这两个三角形的周长比为2:3； B . 如果两个三角形相似，相似比为4:9，那么这两个三角形的周长比为4:9； C . 如果两个三角形相似，相似比为4:9，那么这两个三角形的面积比为2:3； D . 如果两个三角形相似，相似比为4:9，那么这两个三角形的面积比为4:9.

查看解析收藏纠错

+选题
2. 已知△ABC∽△A'B'C'，AD和A'D'是它们的对应中线，若AD＝10，A'D'＝6，则△ABC与△A'B'C'的周长比是（）

A . 3：5 B . 9：25 C . 5：3 D . 25：9

查看解析收藏纠错

+选题
3. 如图，在 $\text{[math]}$ ABCD中，点E在对角线BD上，EM∥AD，交AB于点M，EN∥AB，交AD于点N，则下列式子一定正确的是( ）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图，在△ABC中，D，E分别是AB，AC边上的点，DE∥BC，若AD＝2，AB＝3，DE＝4，则BC等于（）

A . 5 B . 6 C . 7 D . 8

查看解析收藏纠错

+选题
5. 如图，在一斜边长30cm的直角三角形木板(即Rt△ACB)中截取一个正方形CDEF，点D在边BC上，点E在斜边AB上，点F在边AC上，若AF：AC=1：3，则这块木板截取正方形CDEF后，剩余部分的面积为（）

A . 200cm² B . 170cm² C . 150cm² D . 100 cm²

查看解析收藏纠错

+选题
6. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上的一点，且 $\text{[math]}$ ．若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

7. 三个形状大小相同的菱形按如图所示方式摆放，已知∠AOB＝∠AOE＝90°，菱形的较短对角线长为2cm．若点C落在AH的延长线上，则△ABE的周长为cm．

查看解析收藏纠错

+选题

三、综合题

8. 小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．

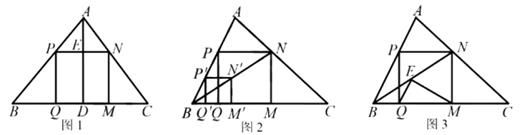
请帮助小波解决“温故”、“推理”、“拓展”中的问题．

（1）温故：如图1，在△ $\text{[math]}$ 中， $\text{[math]}$ ⊥ $\text{[math]}$ 于点 $\text{[math]}$ ，正方形 $\text{[math]}$ 的边 $\text{[math]}$ 在 $\text{[math]}$ 上，顶点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ ， $\text{[math]}$ 上，若 BC=a，AD=h，求正方形 $\text{[math]}$ 的边长(a，h表示)．

（2）操作：如何能画出这个正方形PQMN呢?
如图2，小波画出了图1的△ABC，然后按数学家波利亚在《怎样解题》中的方法进行操作，先在AB上任取一点 $\text{[math]}$ ，画正方形 $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 边上， $\text{[math]}$ 在△ $\text{[math]}$ 内，然后连结 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点N，画 $\text{[math]}$ ⊥ $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ⊥ $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ⊥ $\text{[math]}$ 于点 $\text{[math]}$ ，得到四边形P $\text{[math]}$ ．

推理：证明图2中的四边形 $\text{[math]}$ 是正方形．

（3）拓展：小波把图2中的线段BN称为“波利亚线”，在该线截取 $\text{[math]}$ ，连结 $\text{[math]}$ ， $\text{[math]}$ (如图3)．当∠ $\text{[math]}$ =90°时，求“波利亚线”BN的长（用a、h表示）．

查看解析收藏纠错

+选题
9. 如图①，在正方形ABCD中，AB=6，M为对角线BD上任意一点(不与B、D重合)，连接CM，过点M作MN⊥CM，交线段AB于点N

（1）求证：MN=MC；

（2）若DM：DB=2：5，求证：AN=4BN；

（3）如图②，连接MC交BD于点G.若BG：MG=3：5，求NG·CG的值

查看解析收藏纠错

+选题
10. 综合与实践
折纸是同学们喜欢的手工活动之一，通过折纸我们既可以得到许多美丽的图形，同时折纸的过程还蕴含着丰富的数学知识．

折一折：把边长为4的正方形纸片ABCD对折，使边AB与CD重合，展开后得到折痕EF，如图①；点M为CF上一点，将正方形纸片ABCD沿直线DM折叠，使点C落在EF上的点N处，展开后连接DN，MN，AN，如图②．

（1） (一)填一填，做一做：
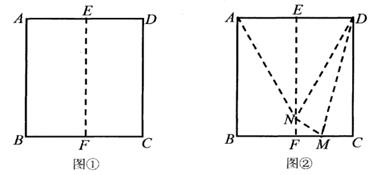
图②中，∠CMD= °；线段NF= ；

（2）图②中，试判断△AND的形状，并给出证明．
剪一剪、折一折：将图②中的△AND剪下来，将其沿直线GH折叠，使点A落在点A’处，分别得到图③、图④．

（3） (二)填一填：
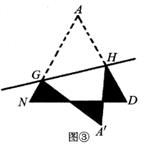
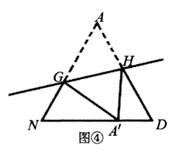
图③中阴影部分的周长为；

（4）图③中，若∠A'GN=80°，则∠A'HD=°；

（5）图③中的相似三角形(包括全等三角形)共有对；

（6）如图④点A'落在边ND上，若 $\text{[math]}$ ，则 $\text{[math]}$ = (用含m，n的代数式表示)．

查看解析收藏纠错

+选题

初中数学华师大版九年级上学期 第23章 23.3.3 相似三角形的性质

一、单选题

二、填空题

三、综合题

相关试卷 收起∨

初中数学华师大版九年级上学期第23章 23.3.3 相似三角形的性质

相关试卷收起∨