北京市2019年中考数学试卷

修改时间：2021-05-20 浏览次数：1151 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 4月24日是中国航天日，1970年的这一天，我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射，标志着中国从此进入了太空时代，它的运行轨道，距地球最近点439 000米．将439 000用科学记数法表示应为（）

A . 0.439×10⁶ B . 4.39×10⁶ C . 4.39×10⁵ D . 139×10³

查看解析收藏纠错

+选题
2. 下列倡导节约的图案中，是轴对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 正十边形的外角和为（）

A . 180° B . 360° C . 720° D . 1440°

查看解析收藏纠错

+选题
4. 在数轴上，点A，B在原点O的两侧，分别表示数a ， 2，将点A向右平移1个单位长度，得到点C．若CO=BO，则a的值为（）

A . -3 B . -2 C . -1 D . 1

查看解析收藏纠错

+选题
5. 已知锐角∠AOB如图，（1）在射线OA上取一点C，以点O为圆心，OC长为半径作 $\text{[math]}$ ，交射线OB于点D，连接CD；（2）分别以点C，D为圆心，CD长为半径作弧，交 $\text{[math]}$ 于点M，N；（3）连接OM，MN．
根据以上作图过程及所作图形，下列结论中错误的是（）

A . ∠COM=∠COD B . 若OM=MN，则∠AOB=20° C . MN∥CD D . MN=3CD

查看解析收藏纠错

+选题
6. 如果 $\text{[math]}$ ，那么代数式 $\text{[math]}$ 的值为（）

A . -3 B . -1 C . 1 D . 3

查看解析收藏纠错

+选题
7. 用三个不等式 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中的两个不等式作为题设，余下的一个不等式作为结论组成一个命题，组成真命题的个数为（）

A . 0 B . 1 C . 2 D . 3

查看解析收藏纠错

+选题

8. 某校共有200名学生，为了解本学期学生参加公益劳动的情况，收集了他们参加公益劳动时间（单位：小时）等数据，以下是根据数据绘制的统计图表的一部分．

学生类型人数时间		$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
性别	男	7	31	25	30	4
性别	女	8	29	26	32	8
学段	初中		25	36	44	11
学段	高中

下面有四个推断：①这200名学生参加公益劳动时间的平均数一定在24.5-25.5之间②这200名学生参加公益劳动时间的中位数在20-30之间③这200名学生中的初中生参加公益劳动时间的中位数一定在20-30之间④这200名学生中的高中生参加公益劳动时间的中位数可能在20-30之间所有合理推断的序号是（）

A . ①③ B . ②④ C . ①②③ D . ①②③④

查看解析收藏纠错

+选题

二、填空题

9. 若分式 $\text{[math]}$ 的值为0，则 $\text{[math]}$ 的值为.

查看解析收藏纠错

+选题
10. 如图，已知△ABC，通过测量、计算得△ABC的面积约为cm².（结果保留一位小数）

查看解析收藏纠错

+选题
11. 在如图所示的几何体中，其三视图中有矩形的是.（写出所有正确答案的序号）

查看解析收藏纠错

+选题
12. 如图所示的网格是正方形网格，则 $\text{[math]}$ ＝°（点A，B，P是网格线交点）.

查看解析收藏纠错

+选题
13. 在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ 在双曲线 $\text{[math]}$ 上．点 $\text{[math]}$ 关于 $\text{[math]}$ 轴的对称点 $\text{[math]}$ 在双曲线 $\text{[math]}$ 上，则 $\text{[math]}$ 的值为.

查看解析收藏纠错

+选题
14. 把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为．

查看解析收藏纠错

+选题
15. 小天想要计算一组数据92，90，94，86，99，85的方差 $\text{[math]}$ ．在计算平均数的过程中，将这组数据中的每一个数都减去90，得到一组新数据2，0，4， $\text{[math]}$ 4，9， $\text{[math]}$ 5．记这组新数据的方差为 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ . (填“ $\text{[math]}$ ”，“ $\text{[math]}$ ”或“ $\text{[math]}$ ”)

查看解析收藏纠错

+选题
16. 在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合）．对于任意矩形ABCD，下面四个结论中，①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形．所有正确结论的序号是．

查看解析收藏纠错

+选题

三、解答题

17. 计算： $\text{[math]}$ .

查看解析收藏纠错

+选题
18. 解不等式组： $\text{[math]}$

查看解析收藏纠错

+选题
19. 关于x的方程 $\text{[math]}$ 有实数根，且m为正整数，求m的值及此时方程的根．

查看解析收藏纠错

+选题
20. 如图，在菱形ABCD中，AC为对角线，点E，F分别在AB，AD上，BE=DF，连接EF．

（1）求证：AC⊥EF；

（2）延长EF交CD的延长线于点G，连接BD交AC于点O，若BD=4，tanG= $\text{[math]}$ ，求AO的长．

查看解析收藏纠错

+选题
21. 国家创新指数是反映一个国家科学技术和创新竞争力的综合指数．对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析．下面给出了部分信息：
a．国家创新指数得分的频数分布直方图（数据分成7组：

30≤x＜40，40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）；

b．国家创新指数得分在60≤x＜70这一组的是：61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5

c.40个国家的人均国内生产总值和国家创新指数得分情况统计图：

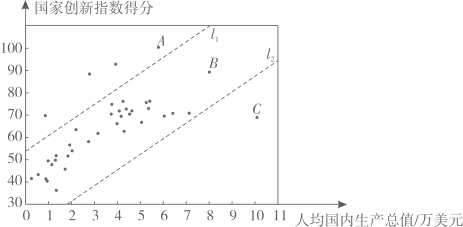
d．中国的国家创新指数得分为69.5.

（以上数据来源于《国家创新指数报告（2018）》）

根据以上信息，回答下列问题：

（1）中国的国家创新指数得分排名世界第；

（2）在40个国家的人均国内生产总值和国家创新指数得分情况统计图中，包括中国在内的少数几个国家所对应的点位于虚线 $\text{[math]}$ 的上方．请在图中用“ $\text{[math]}$ ”圈出代表中国的点；

（3）在国家创新指数得分比中国高的国家中，人均国内生产总值的最小值约为万美元；（结果保留一位小数）

（4）下列推断合理的是．
①相比于点A，B所代表的国家，中国的国家创新指数得分还有一定差距，中国提出“加快建设创新型国家”的战略任务，进一步提高国家综合创新能力；

②相比于点B，C所代表的国家，中国的人均国内生产总值还有一定差距，中国提出“决胜全面建成小康社会”的奋斗目标，进一步提高人均国内生产总值．

查看解析收藏纠错

+选题
22. 在平面内，给定不在同一直线上的点A，B，C，如图所示．点O到点A，B，C的距离均等于a（a为常数），到点O的距离等于a的所有点组成图形G， $\text{[math]}$ 的平分线交图形G于点D，连接AD，CD．

（1）求证：AD=CD；

（2）过点D作DE $\text{[math]}$ BA，垂足为E，作DF $\text{[math]}$ BC，垂足为F，延长DF交图形G于点M，连接CM．若AD=CM，求直线DE与图形G的公共点个数．

查看解析收藏纠错

+选题

23. 小云想用7天的时间背诵若干首诗词，背诵计划如下：

①将诗词分成4组，第i组有 $\text{[math]}$ 首，i =1，2，3，4；

②对于第i组诗词，第i天背诵第一遍，第（ $\text{[math]}$ ）天背诵第二遍，第（ $\text{[math]}$ ）天背诵第三遍，三遍后完成背诵，其它天无需背诵， $\text{[math]}$ 1，2，3，4；

	第1天	第2天	第3天	第4天	第5天	第6天	第7天
第1组	$\text{[math]}$	$\text{[math]}$		$\text{[math]}$
第2组		$\text{[math]}$	$\text{[math]}$		$\text{[math]}$
第3组
第4组				$\text{[math]}$	$\text{[math]}$		$\text{[math]}$

③每天最多背诵14首，最少背诵4首．

解答下列问题：

（1）填入 $\text{[math]}$ 补全上表；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的所有可能取值为；

（3） 7天后，小云背诵的诗词最多为首．

查看解析收藏纠错

+选题

24. 如图，P是 $\text{[math]}$ 与弦AB所围成的图形的外部的一定点，C是 $\text{[math]}$ 上一动点，连接PC交弦AB于点D．

小腾根据学习函数的经验，对线段PC，PD，AD的长度之间的关系进行了探究．

下面是小腾的探究过程，请补充完整：

（1）对于点C在 $\text{[math]}$ 上的不同位置，画图、测量，得到了线段PC，PD，AD的长度的几组值，如下表：

	位置1	位置2	位置3	位置4	位置5	位置6	位置7	位置8
PC/cm	3.44	3.30	3.07	2.70	2.25	2.25	2.64	2.83
PD/cm	3.44	2.69	2.00	1.36	0.96	1.13	2.00	2.83
AD/cm	0.00	0.78	1.54	2.30	3.01	4.00	5.11	6.00

在PC，PD，AD的长度这三个量中，确定的长度是自变量，的长度和的长度都是这个自变量的函数；

（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；

（3）结合函数图象，解决问题：当PC=2PD时，AD的长度约为cm．

查看解析收藏纠错

+选题

25. 在平面直角坐标系 $\text{[math]}$ 中，直线l： $\text{[math]}$ 与直线 $\text{[math]}$ ，直线 $\text{[math]}$ 分别交于点A，B，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ．

（1）求直线 $\text{[math]}$ 与 $\text{[math]}$ 轴的交点坐标；

（2）横、纵坐标都是整数的点叫做整点．记线段 $\text{[math]}$ 围成的区域（不含边界）为 $\text{[math]}$ ．
①当 $\text{[math]}$ 时，结合函数图象，求区域 $\text{[math]}$ 内的整点个数；

②若区域 $\text{[math]}$ 内没有整点，直接写出 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题
26. 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点A，将点A向右平移2个单位长度，得到点B，点B在抛物线上．

（1）求点B的坐标（用含 $\text{[math]}$ 的式子表示）；

（2）求抛物线的对称轴；

（3）已知点 $\text{[math]}$ ， $\text{[math]}$ ．若抛物线与线段PQ恰有一个公共点，结合函数图象，求 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题
27. 已知 $\text{[math]}$ ，H为射线OA上一定点， $\text{[math]}$ ，P为射线OB上一点，M为线段OH上一动点，连接PM，满足 $\text{[math]}$ 为钝角，以点P为中心，将线段PM顺时针旋转 $\text{[math]}$ ，得到线段PN，连接ON．

（1）依题意补全图1；

（2）求证： $\text{[math]}$ ；

（3）点M关于点H的对称点为Q，连接QP．写出一个OP的值，使得对于任意的点M总有ON=QP，并证明．

查看解析收藏纠错

+选题
28. 在△ABC中， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ 两边的中点，如果 $\text{[math]}$ 上的所有点都在△ABC的内部或边上，则称 $\text{[math]}$ 为△ABC的中内弧．例如，下图中 $\text{[math]}$ 是△ABC的一条中内弧．

（1）如图，在Rt△ABC中， $\text{[math]}$ 分别是 $\text{[math]}$ 的中点．画出△ABC的最长的中内弧 $\text{[math]}$ ，并直接写出此时 $\text{[math]}$ 的长；

（2）在平面直角坐标系中，已知点 $\text{[math]}$ ，在△ABC中， $\text{[math]}$ 分别是 $\text{[math]}$ 的中点．
①若 $\text{[math]}$ ，求△ABC的中内弧 $\text{[math]}$ 所在圆的圆心 $\text{[math]}$ 的纵坐标的取值范围；

②若在△ABC中存在一条中内弧 $\text{[math]}$ ，使得 $\text{[math]}$ 所在圆的圆心P在△ABC的内部或边上，直接写出t的取值范围．

查看解析收藏纠错

+选题

北京市2019年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨