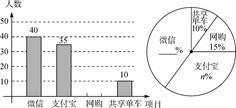
修改时间:2024-07-13 浏览次数:249 类型:月考试卷
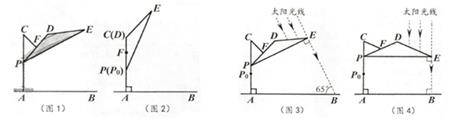
如图1,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD中点,AC=2.8m,PD=2m,CF=1m,∠DPE=20°。当点P位于初始位置P0时,点D与C重合(图2),根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳。

①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)
试题篮