修改时间:2021-05-20 浏览次数:731 类型:中考模拟
婆罗摩笈多(Brahmagupta),是一位印度数学家和天文学家,书写了两部关于数学和天文学的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数概念及加减法运算仅晚于中国《九章算术》,而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及部分证明过程如下:
已知:如图1,四边形ABCD内接于⊙O,对角线AC⊥BD于点P,PM⊥AB于点M,延长MP交CD于点N,求证:CN=DN.
证明:在△ABP和△BMP中,∵AC⊥BD,PM⊥AB,
∴∠BAP+∠ABP=90°,∠BPM+∠MBP=90°.
∴∠BAP=∠BPM.
∵∠DPN=∠BPM,∠BAP=∠BDC.
∴…

类别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 城中村燃煤问题 | 15% |
D | 其他(绿化不足等) | n |

LED灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图1,在矩形纸片ABCD和矩形纸片EFGH中,AB=1,AD=2,且EF>AD,FG>AB,点E是AD的中点,矩形纸片EFGH以点E为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.

如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD.
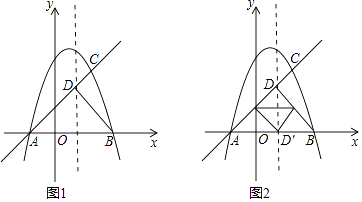
试题篮