2016-2017学年辽宁省大连市甘井子区八年级上学期期末数学试卷

1. 下列图形中，不是轴对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
2. 计算（ $\text{[math]}$ ）^﹣¹的结果是（）

A . $\text{[math]}$ B . 2 C . ﹣2 D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
3. 下列运算中正确的是（　　）

A . 2x+3y=5xy B . x⁸÷x²=x⁴ C . （x²y）³=x⁶y³ D . 2x³•x²=2x⁶

查看解析收藏纠错

+选题
4. 如图，在Rt△ABC中，∠A=30°，CD=CB，则∠ABD的度数是（）

A . 15° B . 20° C . 30° D . 60°

查看解析收藏纠错

+选题
5.
如图，在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD=（）

A . 36° B . 54° C . 18° D . 64°

查看解析收藏纠错

+选题
6. 如图，一个等边三角形纸片剪去一个角后变成一个四边形，则图中∠1+∠2的度数为（）

A . 180° B . 220° C . 240° D . 300°

查看解析收藏纠错

+选题
7. 如图，在Rt△ABC中，∠ACB=90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处，若∠A=25°，则∠ADE的度数为（）

A . 20° B . 30° C . 40° D . 50°

查看解析收藏纠错

+选题
8. 如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）

A . ∠A=∠C B . AD=CB C . BE=DF D . AD∥BC

查看解析收藏纠错

+选题

9. 若分式 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是．

查看解析收藏纠错

+选题
10. 分解因式：3a³﹣12a=．

查看解析收藏纠错

+选题
11. 若点M（a，3）和点N（2，a+b）关于x轴对称，则b的值为．

查看解析收藏纠错

+选题
12. 计算：（a^﹣¹b²）³=．

查看解析收藏纠错

+选题
13. 若x=3是分式方程 $\text{[math]}$ =0的根，则a的值是．

查看解析收藏纠错

+选题
14. 如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC的周长是．

查看解析收藏纠错

+选题
15. 如图，△ABC≌△DEF，点F在BC边上，AB与EF相交于点P．若∠DEF=40°，PB=PF，则∠APF=°．

查看解析收藏纠错

+选题
16. 如图，边长为a、b的矩形，它的周长为14，面积为10，则a²b+ab²的值为．

查看解析收藏纠错

+选题

17. 计算：

（1）（15x²y﹣10xy²）÷5xy

（2）（4y﹣1）（5﹣y）

查看解析收藏纠错

+选题
18. 先化简，再选择一个你喜欢的数字代入求值：（ $\text{[math]}$ ﹣ $\text{[math]}$ ）÷ $\text{[math]}$ ．

查看解析收藏纠错

+选题
19. 如图，点F、C在BE上，BF=CE，AB=DE，∠B=∠E．
求证：∠A=∠D．

查看解析收藏纠错

+选题
20.
已知平面直角坐标系中，点A（﹣3，3）、B（﹣2，﹣2）．

（1）请在如图所示的网格平面内作出平面直角坐标系；

（2）请直接写出点C的坐标为．

（3）请画出△ABC关于y轴对称的△A₁B₁C₁ ，并直接写出A₁、B₁、C₁的坐标．

查看解析收藏纠错

+选题

21. 如图，在△ABC中，AB=AC，BD、CE是腰AB、AC上的高，交于点O．

（1）求证：OB=OC．

（2）若∠ABC=65°，求∠COD的度数．

查看解析收藏纠错

+选题
22. 列方程解应用题
八年级学生去距学校10km的博物馆参观，一部分学生骑自行车先走，过了20min后，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度．

查看解析收藏纠错

+选题
23. 已知关于x的分式方程 $\text{[math]}$ + $\text{[math]}$ =1（a≠2且a≠3）的解为正数，求字母a的取值范围．

查看解析收藏纠错

+选题

24.
“作差法”是常见的比较代数式大小的一种方法，即要比较代数式M、N的大小，只要作出它们的差M﹣N，若M﹣N＞0，则M＞N；若M﹣N=0，则M=N；若M﹣N＜0，则M＜N．

（1）如图1，把边长为a+b（a≠b）的大正方形分割成两个边长分别是a、b的小正方形及两个长方形，试比较来两个小正方形面积之和M与两个长方形面积之和N的大小．

（2）如图2，图3，△ABC中，AD⊥BC于D，AD=BC=2x﹣y，长方形EFGH中，长EH=2x﹣ $\text{[math]}$ y，宽EF=y，△ABC与长方形EFGH的面积分别为M、N，试比较M、N的大小，其中y＞0，x＞ $\text{[math]}$ y且x≠y．

查看解析收藏纠错

+选题
25.
如图，长方形ABCD中，AB=6cm，BC=4cm，点P从点A出发（不含点A），沿A→B→C→D运动，同时，点Q从点B出发（不含点B），沿B→C→D运动，当点P到达点B时，点Q恰好到达点C，已知点P每秒比点Q每秒多运动1cm，当其中一点到达点D（不含点D）时，另一点停止运动．

（1）求P、Q两点的速度；

（2）当其中一点到达点D时，另一点距离D点 cm（直接写答案）；

（3）设点P、Q的运动时间为t（x），请用含t的代数式表示△APQ的面积为S（cm³），并写出t的取值范围．

查看解析收藏纠错

+选题
26. 阅读下列材料：
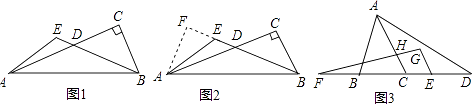
如图1，在Rt△ABC中，∠C=90°，D为边AC上一点，DA=DB，E为BD延长线上一点，∠AEB=120°，猜想AC、BE、AE的数量关系，并证明．
小明的思路是：根据等腰△ADB的轴对称性，将整个图形沿着AB边的垂直平分线翻折，得到点C的对称点F，如图2，过点A作AF⊥BE，交BE的延长线于F，请补充完成此问题；
参考小明思考问题的方法，解答下列问题：
如图3，等腰△ABC中，AB=AC，D、F在直线BC上，DE=BF，连接AD，过点E作EG∥AC交FH的延长线于点G，∠DFG+∠D=∠BAC．

（1）探究∠BAD与∠CHG的数量关系；

（2）请在图中找出一条和线段AD相等的线段，并证明．

查看解析收藏纠错

+选题

2016-2017学年辽宁省大连市甘井子区八年级上学期期末数学试卷

一、选择题

二、填空题

三、解答题

四、解答题

五、解答题

相关试卷收起∨

2016-2017学年辽宁省大连市甘井子区八年级上学期期末数学试卷

一、选择题

二、填空题

三、解答题

四、解答题

五、解答题

相关试卷 收起∨

相关试卷收起∨