2015-2016学年河南省周口市周口港区八年级下学期期中数学试卷

1. 下列各式与 $\text{[math]}$ 是同类二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 要使二次根式 $\text{[math]}$ 有意义，x必须满足（）

A . x≤2 B . x≥2 C . x＞2 D . x＜2

查看解析收藏纠错

+选题
3. 实数a在数轴上的位置如图所示，则化简|1﹣a|+ $\text{[math]}$ 的结果是（）

A . ﹣1 B . 1 C . 2a﹣3 D . 3﹣2a

查看解析收藏纠错

+选题
4. 在平面直角坐标系中，点P（﹣x，2x）到原点O的距离等于5，则x的值是（）

A . ±1 B . 1 C . $\text{[math]}$ D . ± $\text{[math]}$

查看解析收藏纠错

+选题
5. 等腰三角形的腰长为5，底边长为8，则该三角形的面积等于（）

A . 6 B . 12 C . 24 D . 40

查看解析收藏纠错

+选题
6. 如图，四边形ABCD的对角线AC和BD交于点O，则下列不能判断四边形ABCD是平行四边形的条件是（）

A . OA=OC，AD∥BC B . ∠ABC=∠ADC，AD∥BC C . AB=DC，AD=BC D . ∠ABD=∠ADB，∠BAO=∠DCO

查看解析收藏纠错

+选题
7. 如图，在四边形ABCD的外侧，以四边形的边为边分别作四个小正方形，连接相邻的两个顶点，得到四个阴影三角形，则这四个阴影三角形的面积a、b、c、d满足（）

A . a+b=c+d B . a²+b²=c²+d² C . a+c=b+d D . a²+c²=b²+d²

查看解析收藏纠错

+选题

8. 计算： $\text{[math]}$ =．

查看解析收藏纠错

+选题
9. 当m= $\text{[math]}$ 时，代数式m²+2m﹣2的值是．

查看解析收藏纠错

+选题
10. 命题“在同一个三角形中，等边对等角”的逆命题是，是（填“真命题”或“假命题”）

查看解析收藏纠错

+选题
11. 在Rt△ABC中，∠C=90°，∠B=60°，AC=2，则斜边AB的长为．

查看解析收藏纠错

+选题
12. 若▱ABCD的三条边分别为8cm，（x﹣2）cm，（x+3）cm，则该▱ABCD的周长是 cm．

查看解析收藏纠错

+选题
13. 在▱ABCD中，边AB=3，对角线AC=2 $\text{[math]}$ ，BD=4，则▱ABCD的面积等于．

查看解析收藏纠错

+选题
14. 如图，在△ABC中，AB=AC=4，BD是△ABC的中线，∠ADB=120°，点E在中线BD的延长线上，则△ACE是直角三角形时，DE的长为．

查看解析收藏纠错

+选题

15. 计算题：

（1）（ $\text{[math]}$ ） $\text{[math]}$ ；

（2） 4a² $\text{[math]}$ ．

查看解析收藏纠错

+选题
16. 计算：

（1）已知m=1+ $\text{[math]}$ ，n=1﹣ $\text{[math]}$ ，求代数式m²+2mn﹣n²的值；

（2）已知x+ $\text{[math]}$ = $\text{[math]}$ ，求代数式x﹣ $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
17. 如图，在四边形ABCD中，∠D=90°，AB=2，BC=4，CD=AD= $\text{[math]}$ ．

（1）求∠BAD、∠BCD的度数．

（2）求四边形ABCD的面积．

查看解析收藏纠错

+选题
18. 完成下列证明过程，求证：三角形的中位线平行于三角形的第三边，并且等于第三边的一半．
已知：
求证：

查看解析收藏纠错

+选题
19. 如图，在▱ABCD中，∠ADC的平分线交AB于点E，∠ABC的平分线交CD于点F，求证：四边形EBFD是平行四边形．

查看解析收藏纠错

+选题
20. 如图，△ACB与△ECD都是等腰直角三角形，△ACB的顶点A在△ECD的斜边DE上，求证：AE²+AD²=2AC² ．（提示：连接BD）

查看解析收藏纠错

+选题
21. 解答题

（1）在△ABC中，AB、BC、AC三边的长分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，求这个三角形的面积．
如图1，某同学在解答这道题时，先建立一个每个小正方形的边长都是1的网格，再在网格中画出边长符合要求的格点三角形ABC（即△ABC三个顶点都在小正方形的顶点处），这样不需要求△ABC的高，而借用网格就能就算出它的面积．
请你将△ABC的面积直接填写在横线上．

（2）思维拓展：
已知△ABC三边的长分别为 $\text{[math]}$ a（a＞0），求这个三角形的面积．
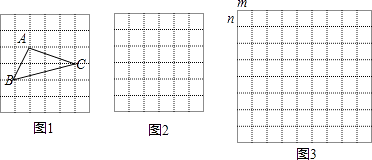
我们把上述求△ABC面积的方法叫做构图法．如图2，网格中每个小正方形的边长都是a，请在网格中画出相应的△ABC，并求出它的面积．

（3）类比创新：
若△ABC三边的长分别为 $\text{[math]}$ （m＞0，n＞0，且m≠n），求出这个三角形的面积．
如图3，网格中每个小长方形长、宽都是m，n，请在网格中画出相应的△ABC，用网格计算这个三角形的面积．

查看解析收藏纠错

+选题
22.
如图，在△ABC中，AC的中点为D，BC的中点为E，F是DE的中点，动点G在边AB上，连接GF，延长GF到点H，使HF=GF，连接HD，HE．

（1）求证：四边形HDGE是平行四边形．

（2）已知∠C=90°，∠A=30°，AB=4．
①当AG为何值时，四边形HDGE是矩形；
②当AG为何值时，四边形HDGE是菱形．

查看解析收藏纠错

+选题

2015-2016学年河南省周口市周口港区八年级下学期期中数学试卷

一、选择题

二、填空题：

三、解答题：

相关试卷收起∨

2015-2016学年河南省周口市周口港区八年级下学期期中数学试卷

一、选择题

二、填空题：

三、解答题：

相关试卷 收起∨

相关试卷收起∨