中考备考专题复习：圆的有关计算

修改时间：2024-08-23 浏览次数：1236 类型：二轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1.
如图，在边长为1的正方形中，以各顶点为圆心，对角线的长的一半为半径在正方形内画弧，则图中阴影部分的面积为（）

A . 2- $\text{[math]}$ π B . $\text{[math]}$ π C . $\text{[math]}$ -1 D . $\text{[math]}$

查看解析收藏纠错

+选题
2.
在△ABC中，∠C为锐角，分别以AB，AC为直径作半圆，过点B，A，C作弧BAC，如图所示．若AB=4，AC=2，S₁-S₂= $\text{[math]}$ ，则S₃-S₄的值是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3.
如图所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区．∠AOB=90°，弧AB的半径OA长是6米，C是OA的中点，点D在弧AB上，CD∥OB，则图中休闲区(阴影部分)的面积是(　　)

A . $\text{[math]}$ 米² B . $\text{[math]}$ 米² C . $\text{[math]}$ 米² D . $\text{[math]}$ 米²

查看解析收藏纠错

+选题
4.
如图，⊙O中，半径OA=4，∠AOB=120°，用阴影部分的扇形围成的圆锥底面圆的半径长是（）.

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

查看解析收藏纠错

+选题
5.
如图，正方形ABCD的边长为1，分别以顶点A、B、C、D为圆心，1为半径画弧，四条弧交于点E、F、G、H，则图中阴影部分的外围周长为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . π D . $\text{[math]}$ π

查看解析收藏纠错

+选题
6.
如图，直径AB为6的半圆，绕A点逆时针旋转60°，此时点B到了点B′，则图中阴影部分的面积是（　　）

A . 3π B . 6π C . 5π D . 4π

查看解析收藏纠错

+选题
7. 如图，圆锥的底面半径r为6cm，高h为8cm，则圆锥的侧面积为（）

A . 30πcm² B . 48πcm² C . 60πcm² D . 80πcm²

查看解析收藏纠错

+选题
8.
如图，是一圆锥的左视图，根据图中所标数据，圆锥侧面展开图的扇形圆心角的大小为（　　）

A . 90° B . 120° C . 135° D . 150°

查看解析收藏纠错

+选题
9.
如图，从一张腰长为60cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的高为（　　）

A . 10cm B . 15cm C . 10 $\text{[math]}$ cm D . 20 $\text{[math]}$ cm

查看解析收藏纠错

+选题
10. 半径为6，圆心角为120°的扇形的面积是（　　）

A . 3π B . 6π C . 9π D . 12π

查看解析收藏纠错

+选题
11.
如图，有一内部装有水的直圆柱形水桶，桶高20公分；另有一直圆柱形的实心铁柱，柱高30公分，直立放置于水桶底面上，水桶内的水面高度为12公分，且水桶与铁柱的底面半径比为2：1．今小贤将铁柱移至水桶外部，过程中水桶内的水量未改变，若不计水桶厚度，则水桶内的水面高度变为多少公分？（　　）

A . 4.5 B . 6 C . 8 D . 9

查看解析收藏纠错

+选题
12. 如图，边长为4的正方形ABCD内接于点O，点E是 $\text{[math]}$ 上的一动点（不与A、B重合），点F是 $\text{[math]}$ 上的一点，连接OE、OF，分别与AB、BC交于点G，H，且∠EOF=90°，有以下结论，其中正确的个数是（）.
① $\text{[math]}$ = $\text{[math]}$ ； ②△OGH是等腰三角形； ③四边形OGBH的面积随着点E位置的变化而变化；④△GBH周长的最小值为4+ $\text{[math]}$ .

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题

二、填空题

13. 一个侧面积为16 $\text{[math]}$ πcm²的圆锥，其主视图为等腰直角三角形，则这个圆锥的高为cm．

查看解析收藏纠错

+选题
14.
如图所示的两段弧中，位于上方的弧半径为r_上，下方的弧半径为r_下，则r_上r_下．（填“＜”“=”“＜”）

查看解析收藏纠错

+选题
15.
如图，△ABC是⊙O的内接正三角形，⊙O的半径为3，则图中阴影部分的面积是．

查看解析收藏纠错

+选题
16.
如图，AB是⊙O的直径，AC是⊙O的弦，过点C的切线交AB的延长线于点D，若∠A=∠D，CD=3，则图中阴影部分的面积为．

查看解析收藏纠错

+选题
17.
如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最大值是．

查看解析收藏纠错

+选题

三、综合题

18.
如图，△ABC内接于⊙O，BD为⊙O的直径，BD与AC相交于点H，AC的延长线与过点B的直线相交于点E，且∠A=∠EBC．

（1）求证：BE是⊙O的切线；

（2）已知CG∥EB，且CG与BD、BA分别相交于点F、G，若BG•BA=48，FG= $\text{[math]}$ ，DF=2BF，求AH的值．

查看解析收藏纠错

+选题
19.
如图，正方形ABCD的对角线相交于点O，点M，N分别是边BC，CD上的动点（不与点B，C，D重合），AM，AN分别交BD于点E，F，且∠MAN始终保持45°不变．

（1）求证： $\text{[math]}$ = $\text{[math]}$ ；

（2）求证：AF⊥FM；

（3）请探索：在∠MAN的旋转过程中，当∠BAM等于多少度时，∠FMN=∠BAM？写出你的探索结论，并加以证明．

查看解析收藏纠错

+选题
20.
问题背景：
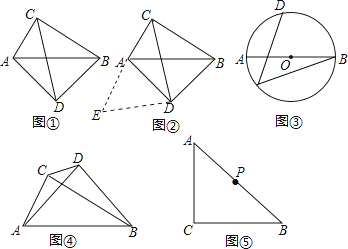
如图①，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．
小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE= $\text{[math]}$ CD，从而得出结论：AC+BC= $\text{[math]}$ CD．
简单应用：

（1）在图①中，若AC= $\text{[math]}$ ，BC=2 $\text{[math]}$ ，则CD=．

（2）如图③，AB是⊙O的直径，点C、D在⊙上， $\text{[math]}$ = $\text{[math]}$ ，若AB=13，BC=12，求CD的长．
拓展规律：

（3）如图④，∠ACB=∠ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD的长（用含m，n的代数式表示）

（4）如图⑤，∠ACB=90°，AC=BC，点P为AB的中点，若点E满足AE= $\text{[math]}$ AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是．

查看解析收藏纠错

+选题
21.
问题探究：
①新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”，其“面线”被该平面图形截得的线段叫做该平面图形的“面径”（例如圆的直径就是圆的“面径”）．
②解决问题

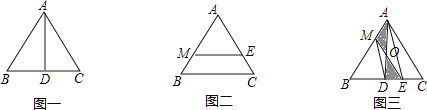
已知等边三角形ABC的边长为2．

（1）如图一，若AD⊥BC，垂足为D，试说明AD是△ABC的一条面径，并求AD的长；

（2）如图二，若ME∥BC，且ME是△ABC的一条面径，求面径ME的长；

（3）如图三，已知D为BC的中点，连接AD，M为AB上的一点（0＜AM＜1），E是DC上的一点，连接ME，ME与AD交于点O，且S_△_MOA=S_△_DOE ．
①求证：ME是△ABC的面径；
②连接AE，求证：MD∥AE；

（4）请你猜测等边三角形ABC的面径长l的取值范围（直接写出结果）

查看解析收藏纠错

+选题
22. 如图，已知四边形ABCD内接于圆O，连结BD，∠BAD=105°，∠DBC=75°．

（1）求证：BD=CD；

（2）若圆O的半径为3，求的长．

查看解析收藏纠错

+选题
23.
如图，在平面直角坐标系中，二次函数y=ax²+bx+c的图象经过点A（﹣1，0），B（0，﹣ $\text{[math]}$ ），C（2，0），其对称轴与x轴交于点D

（1）求二次函数的表达式及其顶点坐标；

（2）若P为y轴上的一个动点，连接PD，则 $\text{[math]}$ PB+PD的最小值为；

（3） M（x，t）为抛物线对称轴上一动点

①若平面内存在点N，使得以A，B，M，N为顶点的四边形为菱形，则这样的点N共有个；

②连接MA，MB，若∠AMB不小于60°，求t的取值范围．

查看解析收藏纠错

+选题

中考备考专题复习：圆的有关计算

一、单选题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨