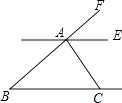
如图,AB∥CD,BE平分∠ABD,DE平分∠BDC,且BE与DE相交于点E,求证∠E=90° 证明:∵AB∥CD({#blank#}1{#/blank#})
∴∠ABD+∠BDC=180°({#blank#}2{#/blank#})
∵BE平分∠ABD({#blank#}3{#/blank#})
∴∠EBD=  {#blank#}4{#/blank#}({#blank#}5{#/blank#})
{#blank#}4{#/blank#}({#blank#}5{#/blank#})
又∵DE平分∠BDC
∴∠BDE=  {#blank#}6{#/blank#}({#blank#}7{#/blank#})
{#blank#}6{#/blank#}({#blank#}7{#/blank#})
∴∠EBD+∠EDB=  ∠ABD+
∠ABD+  ∠BDC({#blank#}8{#/blank#})
∠BDC({#blank#}8{#/blank#})
=  (∠ABD+∠BDC)=90°
(∠ABD+∠BDC)=90°
∴∠E=90°.