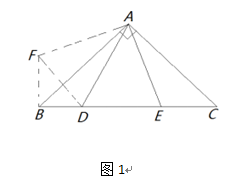
试探究线段BD、CE、DE可以组成什么样的三角形。我们可以过点B作BF⊥BC，使BF=EC，连接AF、DF，易得∠AFB=45°进而得到△AFB≌△AEC，相当于把△AEC绕点A顺时针旋转90°到△AFB，请接着完成下面的推理过程：

∵△AFB≌△AEC，

∴∠BAF=，AF=AE，

∵∠BAC=90°，∠DAE=45°，

∴∠BAD+∠CAE=，

∴∠BAF+∠BAD=45°，

∴∠DAF=45°=，

在△DAF与△DAE中，

AF=AE，

∠DAF=∠DAE，

AD=AD，

∴△DAF≌△DAE，

∴DF=，

∵BD、BF、DF组成直角三角形，

∴BD、CE、DE组成直角三角形.

① 如图②，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，∠ABC+∠ADC=180°，点E在边BC上，点F在边CD上，∠EAF=45°试判断线段BE、DF、EF之间的数量关系，并说明理由。

② 如图③，在①的基础上若点E、F分别在BC和CD的延长线，其他条件不变，①中的关系在图③中是否仍然成立？若成立请说明理由；若不成立请写出新的关系，并说明理由。