2023-2024学年初中数学沪科版九年级下册 24.2.3 圆心角、弧、弦、弦心距之间的关系同步分层训练培优卷

1. 一条弦将圆分成1：3两部分，则劣弧所对的圆心角为（　　）

A . 30° B . 60° C . 90° D . 120°

查看解析收藏纠错

+选题
2. 下列命题正确的是（）

A . 相等的圆心角所对的两条弦相等 B . 圆既是中心对称图形又是轴对称图形 C . 两个圆中，如果弦相等，则弦所对的圆心角也相等 D . 等弧就是长度相等的弧

查看解析收藏纠错

+选题
3. 如图所示，在⊙O中， $\text{[math]}$ ，∠A=30°，则∠B=（）

A . 150° B . 75° C . 60° D . 15°

查看解析收藏纠错

+选题
4. 如图，弧AD是以等边三角形ABC一边AB为半径的四分之一圆周，P为弧AD上任意一点，若AC=5，则四边形ACBP周长的最大值是（）

A . 15 B . 15+5 $\text{[math]}$ C . 20 D . 15+5 $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图，已知 $\text{[math]}$ 的半径为 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 是直径 $\text{[math]}$ 的同侧圆周上的两点， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，动点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，则 $\text{[math]}$ 的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ $\text{[math]}$ C . $\text{[math]}$ $\text{[math]}$ D . $\text{[math]}$ $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，点 $\text{[math]}$ 是 $\text{[math]}$ 的八等分点．若 $\text{[math]}$ ，四边形 $\text{[math]}$ 的周长分别为a，b，则下列正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . a，b大小无法比较

查看解析收藏纠错

+选题
7. 如图， $\text{[math]}$ 是半圆 $\text{[math]}$ 的直径， $\text{[math]}$ 是弦，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 、 $\text{[math]}$ 分别交 $\text{[math]}$ 于点 $\text{[math]}$ 和点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则下列结论中错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

8. 在半径为2的 $\text{[math]}$ 中，弦 $\text{[math]}$ 的长为2，则弦 $\text{[math]}$ 所对的圆心角的度数为．

查看解析收藏纠错

+选题
9. 如图，AB是⊙O的直径，C，D是 $\text{[math]}$ 的三等分点．若∠BOC=40°，则∠AOE的大小是．

查看解析收藏纠错

+选题
10. 如图所示，AB是 $\text{[math]}$ 的直径， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 是弧MB的中点， $\text{[math]}$ 是直径AB上的一动点，若 $\text{[math]}$ ，则 $\text{[math]}$ 的周长的最小值为.

查看解析收藏纠错

+选题
11. 圆 $\text{[math]}$ 的半径为4，AB、CD是 $\text{[math]}$ 的两条弦，且 $\text{[math]}$ ，则 $\text{[math]}$ 最大为．

查看解析收藏纠错

+选题
12. 如图，在以AB为直径的半圆O中，C是半圆的三等分点，点P是弧BC上一动点，连接CP，AP，作OM垂直CP交AP于N，连接BN，若AB＝12，则NB的最小值是．

查看解析收藏纠错

+选题

13. 如图，在半径为5的扇形OAB中，∠AOB=90°，C是 $\text{[math]}$ 上的一个动点(不与点A，B重合)，OD⊥BC，OE⊥AC，垂足分别为点D，E．

（1）当BC=6时，求线段OD的长．

（2）求DE的长．

（3）在△ODE中，是否存在度数不变的角？若存在，请直接指出是哪个角，并求出它的度数．

查看解析收藏纠错

+选题

14. 如图，已知 $\text{[math]}$ 是⊙ $\text{[math]}$ 的直径，且 $\text{[math]}$ ，点 $\text{[math]}$ 在半径 $\text{[math]}$ 上(点 $\text{[math]}$ 与点 $\text{[math]}$ 、点 $\text{[math]}$ 不重合)，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线交⊙ $\text{[math]}$ 于点 $\text{[math]}$ . 连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线交⊙ $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ .

（1）若点 $\text{[math]}$ 是弧BD的中点，求 $\text{[math]}$ 的度数；

（2）求证： $\text{[math]}$ ；

（3）设 $\text{[math]}$ ，则当 $\text{[math]}$ 为何值时 $\text{[math]}$ 的值最大? 最大值是多少?

查看解析收藏纠错

+选题
15. 请阅读下列材料，并完成相应的任务：阿基米德折弦定理，阿基米德（公元前287年一公元前212年），伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家，静态力学和流体静力学的奠基人，并且享有“力学之父”的美称，阿基米德和高斯，牛顿并列为世界三大数学家．
阿拉伯Al-Binmi（973年一1050年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据Al-Binmi译本出版了俄文版《阿基米德全集》，第一题就是阿基米德折弦定理．
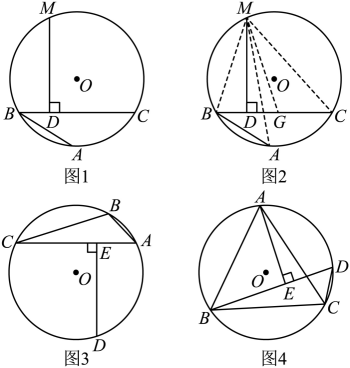
阿基米德折弦定理：如图1，AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC＞AB，M是 $\text{[math]}$ 的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD＝AB+BD．
小明同学运用“截长法”和三角形全等来证明CD＝AB+BD，过程如下：
证明：如图2所示，在CB上截取CG＝AB，连接MA，MB，MC和MG．
∵M是 $\text{[math]}$ 的中点，∴MA＝MC，…

（1）请按照上述思路，写出该证明的剩余部分；

（2）如图3，在⊙O中，BD =CD，DE⊥AC，若AB = 4，AC = 10，则AE的长度为；

（3）如图4，已知等边 $\text{[math]}$ ABC内接于⊙O，AB = 8，D为 $\text{[math]}$ 上一点，∠ABD = 45°，AE⊥BD于点E，求 $\text{[math]}$ BDC的周长．

查看解析收藏纠错

+选题

2023-2024学年初中数学沪科版九年级下册 24.2.3 圆心角、弧、弦、弦心距之间的关系同步分层训练培优卷

一、选择题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

2023-2024学年初中数学沪科版九年级下册 24.2.3 圆心角、弧、弦、弦心距之间的关系 同步分层训练培优卷

一、选择题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

2023-2024学年初中数学沪科版九年级下册 24.2.3 圆心角、弧、弦、弦心距之间的关系同步分层训练培优卷

相关试卷收起∨