2023-2024学年北师大版数学七年级上册3.5探索与表达规律（基础卷）

修改时间：2023-07-31 浏览次数：56 类型：同步测试编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 如图是一个运算程序的示意图，若开始输入x的值为18，则第10次输出的结果为（）

A . 5 B . 0 C . 3 D . 6

查看解析收藏纠错

+选题
2. 下列一组数：1，2，3，4，3，2，1，2，3，4，3，2，1，2，…其中第2022个数是（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
3. 下列图形都是由面积为1的正方形按一定的规律组成的，其中，第1个图形中面积为1的正方形有9个，第2个图形中面积为1的正方形有14个，……，按此规律，则第（）个图形中面积为1的正方形的个数为2024个．

A . 402 B . 403 C . 404 D . 405

查看解析收藏纠错

+选题
4. 正方形ABCD在数轴上的位置如图所示，点D，A对应的数分别为0和1，若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为2；则翻转2019次后，数轴上数2019所对应的点是（　　）

A . 点C B . 点D C . 点A D . 点B

查看解析收藏纠错

+选题
5. 观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗；③中共有11颗星，图形①中共有17颗星，……，按此规律，图形⑦的颗数是（）

A . 43 B . 45 C . 41 D . 536

查看解析收藏纠错

+选题
6. 某人的身份证号码是320922199904010012，此人的生日是（）

A . 9月4日 B . 10月1日 C . 4月1日 D . 9月22日

查看解析收藏纠错

+选题
7. 观察下列各数： $\text{[math]}$ 请根据规律写出第48个数是（）

A . -48 B . 48 C . $\text{[math]}$ D . - $\text{[math]}$

查看解析收藏纠错

+选题
8. 图中有4根绳子，在绳的两端用力拉，有一根绳子是能打成结的，请问是哪一根？（）.

A . B . C . D .

查看解析收藏纠错

+选题
9. 有20个数排成一行，对于任意相邻的三个数，都有中间的数等于前后两数的和.如果第一个数是0，第二个数是2，这20个数的和是（）

A . 2 B . ﹣2 C . 0 D . 4

查看解析收藏纠错

+选题
10. 用同样大小的黑色棋子按如图所示的规律摆放，第1个图形有6颗棋子，第2个图形有9颗棋子，第3个图形有12颗棋子，第4个图形有15颗棋子……，以此类推，第（）个图形有2019颗棋子．

A . 672 B . 673 C . 674 D . 675

查看解析收藏纠错

+选题

二、填空题

11. 观察下列单项式： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，…，则第n个式子是.

查看解析收藏纠错

+选题
12. 如图，下列是一组有规律的图案，它们是由边长相同的小正方形组成，其中部分小正方形涂有阴影，按照这样的规律，第5个图案中有个涂有阴影的小正方形，第n个图案中有个涂有阴影的小正方形（用含有n的式子表示）．

查看解析收藏纠错

+选题
13. 观察下列等式：
$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， ⋯
第1个等式第2个等式第3个等式⋯
按此规律，则第n个等式为．

查看解析收藏纠错

+选题
14. 有理数的乘法运算，除了用乘法口诀外，现有一种“划线法”：如图1，表示的乘法算式是12×23=276；图2表示的是123×24=2952．则图3表示的乘法算式是．

查看解析收藏纠错

+选题
15. 观察下列图形：它们是按一定规律排列的，依照此规律，第2021个图形中共有个五角星．

查看解析收藏纠错

+选题

三、综合题

16. 阅读下列内容，并完成相关问题：
小明说：“我定义了一种新的运算，叫 $\text{[math]}$ (加乘)运算．”然后他写出了一些按照 $\text{[math]}$ (加乘)运算的运算法则进行运算的算式：
(+4)*(+2)＝6；(－4)*(－3)=+7；…
(－5)*(+3)=－8；(+6)*(－7)=－13；…
(+8)*0=8；0*(－9)=9．…
小亮看了这些算式后说：“我知道你定义的 $\text{[math]}$ (加乘)运算的运算法则了．”请你帮助小亮完成下列问题：

（1）归纳 $\text{[math]}$ (加乘)运算的运算法则：
两数进行 $\text{[math]}$ (加乘)运算，．
特别地， $\text{[math]}$ 和任何数进行 $\text{[math]}$ (加乘)运算，或任何数和 $\text{[math]}$ 进行 $\text{[math]}$ (加乘)运算，都得这个数的绝对值．

（2）若有理数的运算顺序适合 $\text{[math]}$ (加乘)运算，请直接写出结果：
①(－3) $\text{[math]}$ (－5)= ；
②(+3) $\text{[math]}$ (－5)=；
③(－9) $\text{[math]}$ (+3) $\text{[math]}$ (－6)=；

（3）试计算：［(－2)*(+3)］*［(－12)*0］(括号的作用与它在有理数运算中的作用一致)；

查看解析收藏纠错

+选题
17. 观察图，解答下列问题．

（1）图中的小圆圈被折线隔开分成六层，第一层有1个小圆圈，第二层有3个圆圈，第三层有5个圆圈，…，第六层有11个圆圈．如果要你继续画下去，那么第八层有几个小圆圈？第n层呢？

（2）某一层上有65个圆圈，这是第几层？

（3）数图中的圆圈个数可以有多种不同的方法．
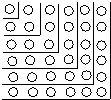
比如：前两层的圆圈个数和为（1+3）或2² ，
由此得，1+3=2² ．
同样，
由前三层的圆圈个数和得：1+3+5=3² ．
由前四层的圆圈个数和得：1+3+5+7=4² ．
由前五层的圆圈个数和得：1+3+5+7+9=5² ．
…
根据上述请你猜测，从1开始的n个连续奇数之和是多少？用公式把它表示出来．

（4）计算：1+3+5+…+99的和；

（5）计算：101+103+105+…+199的和．

查看解析收藏纠错

+选题
18. 观察下列等式：
①3²﹣1²=8×1
②5²﹣3²=8×2
③7²﹣5²=8×3
④9²﹣7²=8×4

（1）请你紧接着写出两个等式：
⑤；
⑥；

（2）利用这个规律计算：2015²﹣2013²的值．

查看解析收藏纠错

+选题
19. 魔术师为大家表演魔术．他请观众想一个数，然后将这个数按以下步骤操作：
魔术师立刻说出观众想的那个数．

（1）如果小明想的数是﹣1，那么他告诉魔术师的结果应该是；

（2）如果小聪想了一个数并告诉魔术师结果为93，那么魔术师立刻说出小聪想的那个数是；

（3）观众又进行了几次尝试，魔术师都能立刻说出他们想的那个数，请你说出其中的奥妙．

查看解析收藏纠错

+选题

20. 观察图形，解答问题：

（1）按下表已填写的形式填写表中的空格：

	图①	图②	图③
三个角上三个数的积	1×（﹣1）×2=﹣2	（﹣3）×（﹣4）×（﹣5）=﹣60
三个角上三个数的和	1+（﹣1）+2=2	（﹣3）+（﹣4）+（﹣5）=﹣12
积与和的商	﹣2÷2=﹣1

（2）请用你发现的规律求出图④中的数y和图⑤中的数x．

查看解析收藏纠错

+选题

2023-2024学年北师大版数学七年级上册3.5探索与表达规律（基础卷）

一、选择题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨