2023年中考数学精选真题实战测试51 圆的基本概念 A

1. 如图， $\text{[math]}$ 内接于 $\text{[math]}$ ，CD是 $\text{[math]}$ 的直径， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 70° B . 60° C . 50° D . 40°

查看解析收藏纠错

+选题
2. 如图，⊙ $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ 是⊙ $\text{[math]}$ 的直径，点P在⊙ $\text{[math]}$ 上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图，AB，CD是 $\text{[math]}$ 的弦，延长AB，CD相交于点P．已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 30° B . 25° C . 20° D . 10°

查看解析收藏纠错

+选题
4. 如图，由边长为1的小正方形构成的网格中，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都在格点上，以 $\text{[math]}$ 为直径的圆经过点 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图，已知 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 边上一点， $\text{[math]}$ ，点 $\text{[math]}$ 为线段 $\text{[math]}$ 的中点，以点 $\text{[math]}$ 为圆心，线段 $\text{[math]}$ 长为半径作弧，交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A . 5 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的两条直径，E是劣弧 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆，且 $\text{[math]}$ ，在弧AB上取点D（不与点A，B重合），连接 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 60° B . 62° C . 72° D . 73°

查看解析收藏纠错

+选题
8. 如图， $\text{[math]}$ 是等边 $\text{[math]}$ 的外接圆，点 $\text{[math]}$ 是弧 $\text{[math]}$ 上一动点（不与 $\text{[math]}$ ， $\text{[math]}$ 重合），下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③当 $\text{[math]}$ 最长时， $\text{[math]}$ ；④ $\text{[math]}$ ，其中一定正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
9. 如图， $\text{[math]}$ 内接于 $\text{[math]}$ ， AD是 $\text{[math]}$ 的直径，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 60° B . 65° C . 70° D . 75°

查看解析收藏纠错

+选题
10. 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 如图，在 $\text{[math]}$ 中，半径 $\text{[math]}$ 垂直弦 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
12. 如图所示，小区内有个圆形花坛O，点C在弦AB上，AC=11，BC=21，OC=13，则这个花坛的面积为．（结果保留 $\text{[math]}$ ）

查看解析收藏纠错

+选题
13. 如图，四边形ABCD内接于⊙O，AB为⊙O的直径，∠ADC=130°，连接AC，则∠BAC的度数为．

查看解析收藏纠错

+选题
14. 如图，A、B、C是 $\text{[math]}$ 上的点， $\text{[math]}$ ，垂足为点D，且D为OC的中点，若 $\text{[math]}$ ，则BC的长为.

查看解析收藏纠错

+选题
15. 如图，在 $\text{[math]}$ 中，AB是 $\text{[math]}$ 的弦， $\text{[math]}$ 的半径为3cm，C为 $\text{[math]}$ 上一点， $\text{[math]}$ ，则AB的长为cm．

查看解析收藏纠错

+选题
16. 如图，AB是 $\text{[math]}$ 的直径，弦CD交AB于点E，连接AC，AD.若 $\text{[math]}$ ，则 $\text{[math]}$ °

查看解析收藏纠错

+选题

17. 如图，C，D是以AB为直径的半圆上的两点， $\text{[math]}$ ，连结BC，CD．

（1）求证： $\text{[math]}$ ．

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求阴影部分的面积．

查看解析收藏纠错

+选题
18. 牂狗江“佘月郎山，西陵晚渡”的风景描绘中有半个月亮挂在山上，月亮之上有个“齐天大圣”守护洞口的传说．真实情况是老王山上有个月亮洞，洞顶上经常有猴子爬来爬去，下图是月亮洞的截面示意图．

（1）科考队测量出月亮洞的洞宽 $\text{[math]}$ 约是28m，洞高 $\text{[math]}$ 约是12m，通过计算截面所在圆的半径可以解释月亮洞像半个月亮，求半径 $\text{[math]}$ 的长（结果精确到0.1m）；

（2）若 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，求 $\text{[math]}$ 的度数，并用数学知识解释为什么“齐天大圣”点 $\text{[math]}$ 在洞顶 $\text{[math]}$ 上巡视时总能看清洞口 $\text{[math]}$ 的情况．

查看解析收藏纠错

+选题
19. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的⊙ $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交线段 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ．

查看解析收藏纠错

+选题
20. 如图，四边形ABCD是⊙O的内接四边形，连接AC，BD，延长CD至点E．

（1）若AB＝AC，求证：∠ADB＝∠ADE；

（2）若BC＝3，⊙O的半径为2，求sin∠BAC．

查看解析收藏纠错

+选题
21. 如图，D是以AB为直径的⊙O上一点，过点D的切线DE交AB的延长线于点E，过点B作BC⊥DE交AD的延长线于点C，垂足为点F.

（1）求证：AB=CB；

（2）若AB=18，sinA= $\text{[math]}$ ，求EF的长.

查看解析收藏纠错

+选题
22.

（1）请在图中作出 $\text{[math]}$ 的外接圆 $\text{[math]}$ （尺规作图，保留作图痕迹，不写作法）；

（2）如图， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，过点 $\text{[math]}$ 的切线与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ .
①求证： $\text{[math]}$ ；
②若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径.

查看解析收藏纠错

+选题
23. （现有若干张相同的半圆形纸片，点 $\text{[math]}$ 是圆心，直径 $\text{[math]}$ 的长是 $\text{[math]}$ ， $\text{[math]}$ 是半圆弧上的一点（点 $\text{[math]}$ 与点 $\text{[math]}$ 、 $\text{[math]}$ 不重合），连接 $\text{[math]}$ 、 $\text{[math]}$ .

（1）沿 $\text{[math]}$ 、 $\text{[math]}$ 剪下 $\text{[math]}$ ，则 $\text{[math]}$ 是三角形（填“锐角”、“直角”或“钝角”）；

（2）分别取半圆弧上的点 $\text{[math]}$ 、 $\text{[math]}$ 和直径 $\text{[math]}$ 上的点 $\text{[math]}$ 、 $\text{[math]}$ .已知剪下的由这四个点顺次连接构成的四边形是一个边长为 $\text{[math]}$ 的菱形.请用直尺和圆规在图中作出一个符合条件的菱形（保留作图痕迹，不要求写作法）；

（3）经过数次探索，小明猜想，对于半圆弧上的任意一点 $\text{[math]}$ ，一定存在线段 $\text{[math]}$ 上的点 $\text{[math]}$ 、线段 $\text{[math]}$ 上的点 $\text{[math]}$ 和直径 $\text{[math]}$ 上的点 $\text{[math]}$ 、 $\text{[math]}$ ，使得由这四个点顺次连接构成的四边形是一个边长为 $\text{[math]}$ 的菱形.小明的猜想是否正确？请说明理由.

查看解析收藏纠错

+选题
24. 综合与实践
“善思”小组开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.

提出问题：

如图1，在线段 $\text{[math]}$ 同侧有两点B，D，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，如果 $\text{[math]}$ ，那么A，B，C，D四点在同一个圆上.

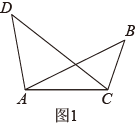
探究展示：

如图2，作经过点A，C，D的 $\text{[math]}$ ，在劣弧 $\text{[math]}$ 上取一点E（不与A，C重合），连接 $\text{[math]}$ ， $\text{[math]}$ 则 $\text{[math]}$ （依据1）

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$ 点A，B，C，E四点在同一个圆上（对角互补的四边形四个顶点共圆）

$\text{[math]}$ 点B，D在点A，C，E所确定的 $\text{[math]}$ 上（依据2）

$\text{[math]}$ 点A，B，C，E四点在同一个圆上

（1）反思归纳：上述探究过程中的“依据1”、“依据2”分别是指什么？
依据1：；依据2：.

（2）图3，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为.

（3）展探究：如图4，已知 $\text{[math]}$ 是等腰三角形， $\text{[math]}$ ，点D在 $\text{[math]}$ 上（不与 $\text{[math]}$ 的中点重合），连接 $\text{[math]}$ .作点C关于 $\text{[math]}$ 的对称点E，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于F，连接 $\text{[math]}$ ， $\text{[math]}$ .

①求证：A，D，B，E四点共圆；

②若 $\text{[math]}$ ， $\text{[math]}$ 的值是否会发生变化，若不变化，求出其值；若变化，请说明理由.

查看解析收藏纠错

+选题

2023年中考数学精选真题实战测试51 圆的基本概念 A

一、单选题（每题3分，共30分）

二、填空题（每空3分，共18分）

三、解答题（共8题，共72分）

相关试卷收起∨

2023年中考数学精选真题实战测试51 圆的基本概念 A

一、单选题（每题3分，共30分）

二、填空题（每空3分，共18分）

三、解答题（共8题，共72分）

相关试卷 收起∨

相关试卷收起∨