2022-2023学年浙教版数学九年级上册4.7 图形的位似同步练习

1. 如图，在平面直角坐标系中，将 $\text{[math]}$ OAB以原点O为位似中心放大后得到 $\text{[math]}$ OCD，若B（0，1），D（0，3），则 $\text{[math]}$ OAB与 $\text{[math]}$ OCD的面积比是（）

A . 2：1 B . 1：3 C . 1：9 D . 9：1

查看解析收藏纠错

+选题
2. 如图，在直角坐标系中，点A在第一象限内，点B在x轴正半轴上，以点O为位似中心，在第三象限内与ΔOAB的位似比为 $\text{[math]}$ 的位似图形ΔOCD.若点C的坐标为 $\text{[math]}$ ，则点A的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图，BC $\text{[math]}$ ED，下列说法不正确的是（）

A . 两个三角形是位似图形 B . 点A是两个三角形的位似中心 C . AB：AC是相似比 D . 点B与点D、点C与点E是对应位似点

查看解析收藏纠错

+选题
4. 如图， $\text{[math]}$ 与 $\text{[math]}$ 位似，点 $\text{[math]}$ 是它们的位似中心，其中 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的面积之比是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1：9

查看解析收藏纠错

+选题
5. 如图， $\text{[math]}$ 与 $\text{[math]}$ 位似，点O是位似中心，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 9 B . 12 C . 16 D . 36

查看解析收藏纠错

+选题
6. 如图，在平面直角坐标系中，△OAB的顶点O在坐标原点，顶点A，B的坐标分别为（－2，－1），（－1.5，0）．△OCD与△OAB位似，位似中心是原点O，若点D的坐标为（4.5，0），则点C的坐标为（）

A . （6，3） B . （－6，－3） C . （4，2） D . （－4，－2）

查看解析收藏纠错

+选题
7. 如图，四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，若OA：OA′＝ $\text{[math]}$ ： $\text{[math]}$ ，则四边形ABCD和A′B′C′D′的面积比为（）

A . $\text{[math]}$ ： $\text{[math]}$ B . 2：3 C . 2：5 D . 4：9

查看解析收藏纠错

+选题
8. 如图，已知△ABC和△A′B′C′是以点C为位似中心的位似图形，且△ABC和△A′B′C′的周长之比为1∶2，点C的坐标为（－1，0），若点B的对应点B′的横坐标为5，则点B的横坐标为（）

A . －5 B . －4 C . $\text{[math]}$ D . －3

查看解析收藏纠错

+选题
9. 如图，在平面直角坐标系中，△ABC的顶点A在第二象限，点B坐标为（﹣2，0），点C坐标为（﹣1，0），以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C．若点A的对应点A′的坐标为（2，﹣3），点B的对应点B′的坐标为（1，0），则点A坐标为（　　）

A . （﹣3，﹣2） B . （﹣2， $\text{[math]}$ ） C . （﹣ $\text{[math]}$ ， $\text{[math]}$ ） D . （﹣ $\text{[math]}$ ， 2）

查看解析收藏纠错

+选题
10. 如图，线段 $\text{[math]}$ 两个端点的坐标分别为 $\text{[math]}$ ，以原点O为位似中心，在第一象限内将线段 $\text{[math]}$ 扩大为原来的2倍后得到线段 $\text{[math]}$ ，则端点C的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 如图，在平面直角坐标系中，已知A（1，0），D（3，0），△ABC与△DEF位似，原点O是位似中心，若AB=2，则DE=.

查看解析收藏纠错

+选题
12. 如图，平面直角坐标系中，点A在 $\text{[math]}$ 轴正半轴上，且 $\text{[math]}$ ， $\text{[math]}$ ，以点 $\text{[math]}$ 为位似中心，将 $\text{[math]}$ 放大2倍，则点 $\text{[math]}$ 的对应点 $\text{[math]}$ 的坐标为.

查看解析收藏纠错

+选题
13. 在平面直角坐标系中，△ABC中点A的坐标是（2，3），以原点O为位似中心把△ABC放大，使放大后的三角形与△ABC的相似比为3：1，则点A的对应点A′的坐标为．

查看解析收藏纠错

+选题
14. 如图，小莉用灯泡 $\text{[math]}$ 照射一个矩形硬纸片 $\text{[math]}$ ，在墙上形成矩形影子 $\text{[math]}$ ，现测得 $\text{[math]}$ ， $\text{[math]}$ ，纸片 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则影子 $\text{[math]}$ 的面积为 $\text{[math]}$ ．

查看解析收藏纠错

+选题
15. 如图，点A（3，4），点B（4，0），以O为位似中心，按比例1∶2，将△AOB放大后得△A₁O₁B₁ ，则A₁坐标为．

查看解析收藏纠错

+选题
16. 在平面直角坐标系中，已知点E（-4，2），F（-2，-2），以原点O为位似中心，相似比为2，把△EFO放大，则点E的对应点E′的坐标是．

查看解析收藏纠错

+选题

17. 放缩尺是一种绘图工具，它能把图形放大或缩小．
制作：把钻有若干等距小孔的四根直尺用螺栓分别在点A，B，C，D处连接起来，使得直尺可以绕着这些点转动，O为固定点， $\text{[math]}$ ， $\text{[math]}$ ，在点A，E处分别装上画笔．
画图：现有一图形M，画图时固定点O，控制点A处的笔尖沿图形M的轮廓线移动，此时点E处的画笔便画出了将图形M放大后的图形N．
原理：
连接 $\text{[math]}$ ， $\text{[math]}$ ，可证得以下结论：
① $\text{[math]}$ 和 $\text{[math]}$ 为等腰三角形，则 $\text{[math]}$ ， $\text{[math]}$ （180°-∠            ▲             ）；
②四边形 $\text{[math]}$ 为平行四边形（理由是            ▲            ）；
③ $\text{[math]}$ ，于是可得O，A，E三点在一条直线上；
④当 $\text{[math]}$ 时，图形N是以点O为位似中心，把图形M放大为原来的            ▲            倍得到的．

查看解析收藏纠错

+选题
18. 如图，以原点O为位似中心，把△OAB放大后得到△OCD，求△OAB与△OCD的相似比.

查看解析收藏纠错

+选题
19. 如图， $\text{[math]}$ 与 $\text{[math]}$ 是位似图形，点O是位似中心， $\text{[math]}$ ， $\text{[math]}$ ，求DE的长.

查看解析收藏纠错

+选题
20. 如图，已知 $\text{[math]}$ 是坐标原点， $\text{[math]}$ 、 $\text{[math]}$ 的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ．

（1）在 $\text{[math]}$ 轴的左侧以 $\text{[math]}$ 为位似中心作 $\text{[math]}$ 的位似 $\text{[math]}$ ，使新图与原图的相似比为 $\text{[math]}$ ；

（2）分别写出 $\text{[math]}$ 、 $\text{[math]}$ 的对应点 $\text{[math]}$ 、 $\text{[math]}$ 的坐标．

查看解析收藏纠错

+选题
21. 如图，在边长为1个单位长度的小正方形组成的网格中，建立如图所示的平面直角坐标系，请按要求完成下面的问题．

（1）以图中的点O为位似中心，将△ABC作位似变换放大到原来的两倍，得到ΔA₁B₁C₁；

（2）若△ABC内一点P的坐标为（a，b），则位似变换后对应的点P'的坐标是；

查看解析收藏纠错

+选题
22. 已知：如图△ABC三个顶点的坐标分别为A（﹣2，﹣2）、B（﹣3，﹣4）、C（﹣1，﹣4），正方形网格中，每个小正方形的边长是1个单位长度.

（1）以点C为位似中心，在网格中画出△A₁B₁C，使△A₁B₁C与△ABC的位似比为2：1，并直接写出点A₁的坐标；

（2） △A₁B₁C与△ABC的面积比为.

查看解析收藏纠错

+选题
23. 阅读与思考
探索位似的性质

利用图形计算器或计算机等信息技术工具，可以很方便地将图形放大或缩小，还可以探索位似的性质．

小明利用几何画板软件，尝试用“观察—猜想-验证—应用”的方法进行探究，步骤如下∶如图（1），任意画一个△ABC，以点O为位似中心，自选新旧图形的相似比为k，得到△A´B´C´．

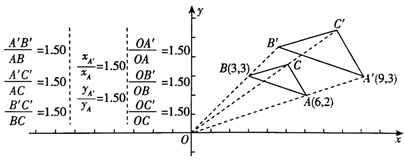
图（1）

第一步，度量对应边的长度，并计算它们的比值，发现结果与k的值相等．

第二步，以0为原点建立平面直角坐标系，分别度量点A，A´的横坐标，并计算比值；分别度量点A，A´的纵坐标，并计算比值，观察比值与k的关系，发现它们相等．接下来对其他顶点进行相同的操作，得出相同的结论．

第三步，作线段 OA，OA´，OB，OB´，OC，OC´，度量它们，发现的结论是：_________．

第四步，任意改变△ABC的位置成形状，发现上面探究得出的结论仍然成立．

于是，小明总结并得出了位似的性质．

任务∶

（1）第三步发现的结论是：．．

（2）已知图（1）中A（6，2），A´（9，3），B（3，3），S_△_ABC=2，则点B´的坐标是，S_△_A´B´C´=．

（3）如图（2），以点A为位似中心，画出与矩形 ABCD的相似比为0.75的一个图形．

查看解析收藏纠错

+选题
24. 如图，已知△ABC顶点的坐标分别为A（1，－1），B（4，－1），C（3，－4）．

（1）将△ABC绕点A逆时针旋转90°后，得到△AB₁C₁ ．在所给的直角坐标系中画出旋转后的 $\text{[math]}$ ，并写出点 $\text{[math]}$ 的坐标： $\text{[math]}$ ；

（2）以坐标原点O为位似中心，在第二象限内再画一个放大的 $\text{[math]}$ ，使得它与△ABC的位似比等于2：1 .

查看解析收藏纠错

+选题

2022-2023学年浙教版数学九年级上册4.7 图形的位似同步练习

一、单选题

二、填空题

三、解答题

相关试卷收起∨

2022-2023学年浙教版数学九年级上册4.7 图形的位似 同步练习

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

2022-2023学年浙教版数学九年级上册4.7 图形的位似同步练习

相关试卷收起∨