安徽省2022年中考数学真题

1. 下列为负数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 0 D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 据统计，2021年我省出版期刊杂志总印数3400万册，其中3400万用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 一个由长方体截去一部分后得到的几何体如图水平放置，其俯视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 下列各式中，计算结果等于 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 甲、乙、丙、丁四个人步行的路程和所用的时间如图所示，按平均速度计算．走得最快的是（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题
6. 两个矩形的位置如图所示，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 已知⊙O的半径为7，AB是⊙O的弦，点P在弦AB上．若PA＝4，PB＝6，则OP＝（）

A . $\text{[math]}$ B . 4 C . $\text{[math]}$ D . 5

查看解析收藏纠错

+选题
8. 随着信息化的发展，二维码已经走进我们的日常生活，其图案主要由黑、白两种小正方形组成．现对由三个小正方形组成的“”进行涂色，每个小正方形随机涂成黑色或白色，恰好是两个黑色小正方形和一个白色小正方形的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 在同一平面直角坐标系中，一次函数 $\text{[math]}$ 与 $\text{[math]}$ 的图像可能是（）

A . B . C . D .

查看解析收藏纠错

+选题
10. 已知点O是边长为6的等边△ABC的中心，点P在△ABC外，△ABC，△PAB，△PBC，△PCA的面积分别记为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ，则线段OP长的最小值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 不等式 $\text{[math]}$ 的解集为．

查看解析收藏纠错

+选题
12. 若一元二次方程 $\text{[math]}$ 有两个相等的实数根，则m=．

查看解析收藏纠错

+选题
13. 如图，平行四边形OABC的顶点O是坐标原点，A在x轴的正半轴上，B，C在第一象限，反比例函数 $\text{[math]}$ 的图象经过点C， $\text{[math]}$ 的图象经过点B．若 $\text{[math]}$ ，则k=．

查看解析收藏纠错

+选题
14. 如图，四边形ABCD是正方形，点E在边AD上，△BEF是以E为直角顶点的等腰直角三角形，EF，BF分别交CD于点M，N，过点F作AD的垂线交AD的延长线于点G．连接DF，请完成下列问题：

（1） $\text{[math]}$ °；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题

15. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
16. 如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点）．

（1）将△ABC向上平移6个单位，再向右平移2个单位，得到 $\text{[math]}$ ，请画出 $\text{[math]}$ ﹔

（2）以边AC的中点O为旋转中心，将△ABC按逆时针方向旋转180°，得到 $\text{[math]}$ ，请画出 $\text{[math]}$ ．

查看解析收藏纠错

+选题
17. 某地区2020年进出口总额为520亿元.2021年进出口总额比2020年有所增加，其中进口额增加了25%，出口额增加了30%．注：进出口总额＝进口额＋出口额．
年份
进口额/亿元
出口额/亿元
进出口总额/亿元
2020
x
y
520
2021
1.25x
1.3y

（1）设2020年进口额为x亿元，出口额为y亿元，请用含x，y的代数式填表：

（2）已知2021年进出口总额比2020年增加了140亿元，求2021年进口额和出口额度分别是多少亿元？

查看解析收藏纠错

+选题
18. 观察以下等式：
第1个等式： $\text{[math]}$ ，
第2个等式： $\text{[math]}$ ，
第3个等式： $\text{[math]}$ ，
第4个等式： $\text{[math]}$ ，
……
按照以上规律．解决下列问题：

（1）写出第5个等式：；

（2）写出你猜想的第n个等式（用含n的式子表示），并证明．

查看解析收藏纠错

+选题
19. 已知AB为⊙O的直径，C为⊙O上一点，D为BA的延长线上一点，连接CD．

（1）如图1，若CO⊥AB，∠D＝30°，OA＝1，求AD的长；

（2）如图2，若DC与⊙O相切，E为OA上一点，且∠ACD＝∠ACE，求证：CE⊥AB．

查看解析收藏纠错

+选题
20. 如图，为了测量河对岸A，B两点间的距离，数学兴趣小组在河岸南侧选定观测点C，测得A，B均在C的北偏东37°方向上，沿正东方向行走90米至观测点D，测得A在D的正北方向，B在D的北偏西53°方向上．求A，B两点间的距离．参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

查看解析收藏纠错

+选题
21. 第24届冬奥会于2022年2月20日在北京胜利闭幕．某校七、八年级各有500名学生．为了解这两个年级学生对本次冬奥会的关注程度，现从这两个年级各随机抽取n名学生进行冬奥会知识测试，将测试成绩按以下六组进行整理（得分用x表示）：
A： $\text{[math]}$ ， B： $\text{[math]}$ ， C： $\text{[math]}$ ，
D： $\text{[math]}$ ， E： $\text{[math]}$ ， F： $\text{[math]}$ ，
并绘制七年级测试成绩频数直方图和八年级测试成绩扇形统计图，部分信息如下：
已知八年级测试成绩D组的全部数据如下：86，85，87，86，85，89，88
请根据以上信息，完成下列问题：

（1） n＝，a＝；

（2）八年级测试成绩的中位数是﹔

（3）若测试成绩不低于90分，则认定该学生对冬奥会关注程度高．请估计该校七、八两个年级对冬奥会关注程度高的学生一共有多少人，并说明理由．

查看解析收藏纠错

+选题
22. 已知四边形ABCD中，BC＝CD．连接BD，过点C作BD的垂线交AB于点E，连接DE．

（1）如图1，若 $\text{[math]}$ ，求证：四边形BCDE是菱形；

（2）如图2，连接AC，设BD，AC相交于点F，DE垂直平分线段AC．
（ⅰ）求∠CED的大小；
（ⅱ）若AF＝AE，求证：BE＝CF．

查看解析收藏纠错

+选题
23. 如图1，隧道截面由抛物线的一部分AED和矩形ABCD构成，矩形的一边BC为12米，另一边AB为2米．以BC所在的直线为x轴，线段BC的垂直平分线为y轴，建立平面直角坐标系xOy，规定一个单位长度代表1米．E（0，8）是抛物线的顶点．

（1）求此抛物线对应的函数表达式；

（2）在隧道截面内（含边界）修建“”型或“”型栅栏，如图2、图3中粗线段所示，点 $\text{[math]}$ ， $\text{[math]}$ 在x轴上，MN与矩形 $\text{[math]}$ 的一边平行且相等．栅栏总长l为图中粗线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， MN长度之和．请解决以下问题：
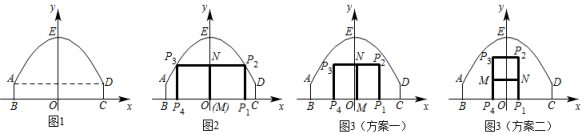
（ⅰ）修建一个“”型栅栏，如图2，点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线AED上．设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ，求栅栏总长l与m之间的函数表达式和l的最大值；
（ⅱ）现修建一个总长为18的栅栏，有如图3所示的修建“”型或“”型栅型两种设计方案，请你从中选择一种，求出该方案下矩形 $\text{[math]}$ 面积的最大值，及取最大值时点 $\text{[math]}$ 的横坐标的取值范围（ $\text{[math]}$ 在 $\text{[math]}$ 右侧）．

查看解析收藏纠错

+选题

安徽省2022年中考数学真题

一、单选题

二、填空题

三、解答题

相关试卷收起∨

年份	进口额/亿元	出口额/亿元	进出口总额/亿元
2020	x	y	520
2021	1.25x	1.3y

安徽省2022年中考数学真题

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨