浙教版备考2022年中考数学二轮复习训练题9：几何应用题

1. 如图，小王在高台上的点A处测得塔底点C的俯角为α，塔顶点D的仰角为β，已知塔的水平距离AB＝a，则此时塔高CD的长为（）

A . asinα+asin β B . atanα+atan β C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图，明年舟山将再添一个最高颜值城市新地标，新城长峙岛上将矗立起一座摩天轮，其直径为90m，旋转1周用时15min．小明从摩天轮的底部（与地面相距0.5m）出发开始观光，摩天轮转动1周，小明在离地面68m以上的空中有多长时间？（）

A . 3min B . 5min C . 6min D . 10min

查看解析收藏纠错

+选题
3. 在科学小实验中，一个边长为30cm正方体小木块沿着一个斜面下滑，其轴截面如图所示.初始状态，正方形的一个顶点与斜坡上的点P重合，点P的高度PF＝40cm，离斜坡底端的水平距离EF＝80cm.正方形下滑后，点B的对应点 $\text{[math]}$ 与初始状态的顶点A的高度相同，则正方形下滑的距离（即 $\text{[math]}$ 的长度）是（）cm

A . 40 B . 60 C . 30 $\text{[math]}$ D . 40 $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图，建筑工地划出了三角形安全区 $\text{[math]}$ ，一人从 $\text{[math]}$ 点出发，沿北偏东53°方向走50m到达C点，另一人从B点出发沿北偏西53°方向走100m到达C点，则点A与点B相距（） $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 130m

查看解析收藏纠错

+选题
5. 某市地铁施工队开始隧道挖掘作业，如图1，圆弧形混凝土管片是构成圆形隧道的重要部件.如图2，有一圆弧形混凝土管片放置在水平地面上，底部用两个完全相同的长方体木块固定，为估计隧洞开挖面的大小，甲、乙两个组对相关数据进行测量，测量结果如下表所示，利用数据能够估算隧道外径 $\text{[math]}$ 大小的组是（）
小组
测量内容
甲
$\text{[math]}$ 的长
乙
$\text{[math]}$ 的长

A . 两组测量数据都不足 B . 甲组 C . 乙组 D . 两组都可以

查看解析收藏纠错

+选题
6. 小明设计了如图所示的树型图案，它是由4个正方形、8个等边三角形和5个扇形组成，其中正方形的边长、等边三角形的边长和扇形的半径均为3，则图中扇形的弧长总和为（）

A . 8π B . $\text{[math]}$ π C . $\text{[math]}$ π D . 12π

查看解析收藏纠错

+选题
7. 如图，学校环保社成员想测得斜坡CD旁一棵树AB的高度，他们先在点C处测得树顶B的仰角为60°，然后在坡顶D测得树顶B的仰角为30°，已知斜坡CD的长度为20m，且坡度为 $\text{[math]}$ ，则树AB的高度是（）

A . $\text{[math]}$ B . 30m C . $\text{[math]}$ D . 40m

查看解析收藏纠错

+选题
8. 如图，为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组根据光的反射定律，利用一面镜子和一根皮尺，设计如下图所示的测量方案：把一面很小的镜子水平放置在离树底B端8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=3.2米，观察者目高CD=1.6米，则树AB的高度约为（）

A . 4.2米 B . 4.8米 C . 6.4米 D . 16.8米

查看解析收藏纠错

+选题
9. 图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，为了测量某建筑物BC的高度，某数学兴趣小组采用了如下的方法：先从与建筑物底端B在同一水平线上的A点出发，先沿斜坡AD行走390米至坡顶D处，再从D处沿水平方向继续前行一定距离后至点E处，在E点处测得该建筑物顶端C的仰角为68°，建筑物底端B的俯角为57°，其中A、B、C、D、E在同一平面内，斜坡AD的坡度i＝1：2.4，根据数学兴趣小组的测量数据，计算得出建筑物BC的高度约为（　　）（计算结果精确到0.1米，参考数据：sin68°≈0.93，tan68°≈2.48，sin57°≈0.84，tan57°≈1.54）

A . 241.6米 B . 391.6米 C . 422.9米 D . 572.9米

查看解析收藏纠错

+选题

11. 某户外遮阳棚如图1，其截面结构示意图如图2所示.支撑柱AB上地面，AB=120 $\text{[math]}$ cm，Р是支撑柱AB上一动点，伞杆CP可绕着中点E旋转，CD=CP=40 $\text{[math]}$ cm，斜拉杆AE可绕点A旋转，AE= $\text{[math]}$ CP．若∠APE=30°，则BP=cm；伞展开长 PD==300cm，若A，C，D在同一条直线上，某时太阳光线恰好与地面垂直，则PD落到地面的阴影长为cm.

查看解析收藏纠错

+选题
12. 现在很多家庭都使用折叠型西餐桌来节省空间，两边翻开后成圆形桌面(如图1)。餐桌两边AD和BC平行且相等(如图2)，小华用皮带尺量出AC=4米，AB=2米，那么桌面翻成圆桌后，桌子面积会增加平方米。(结果保留π)．

查看解析收藏纠错

+选题
13. 一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘，如图所示，AB与CD水平，BC与水平面的夹角为60°，其中AB=60cm，CD=40cm，BC=40cm，那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为cm.

查看解析收藏纠错

+选题
14. 在平面内，机器人完成下列动作：先从点O出发，以每分钟4个单位的速度沿东偏北α（0°≤α≤90°）方向行走t（0≤t≤3）分钟，再向正北方向以同样的速度行走（3﹣t）分钟到达点P，如图所示.则机器人所有可能到达的P点形成的区域的面积为.

查看解析收藏纠错

+选题
15. 如图1是护眼学习台灯，该台灯的活动示意图如图2所示.灯柱BC＝6cm，灯臂AC绕着支点C可以旋转，灯罩呈圆弧形（即 $\text{[math]}$ 和 $\text{[math]}$ ）.在转动过程中，AD（EF）总是与桌面BH平行.当AC⊥BH时，AB＝46cm，DM⊥MH，测得DM＝37.5cm（点M在墙壁M上，且MH⊥BH）；当灯臂AC转到CE位置时，FN⊥MH测得FN＝13.5cm，则点E到桌面BH的距离为cm.若此时点C，F，M在同一条直线上， $\text{[math]}$ 的最低点到桌面BH的距离为35cm，则EF所在圆的半径为cm.

查看解析收藏纠错

+选题
16. 如图，这是一个供滑板爱好者使用的U型池的示意图，该U型池可以看成是长方体去掉一个“半圆柱”而成，中间可供滑行部分的截面是直径为 $\text{[math]}$ 的半圆，其边缘 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ，一滑板爱好者从A点滑到E点，则他滑行的最短距离约为 $\text{[math]}$ .（边缘部分的厚度忽略不计）

查看解析收藏纠错

+选题

17. 如图，海面上产生了一股强台风．台风中心A在某沿海城市B的正西方向，小岛C位于城市B北偏东29°方向上，台风中心沿北偏东60°方向向小岛C移动，此时台合风中心距离小岛200海里．

（1）过点B作 $\text{[math]}$ 于点P，求 $\text{[math]}$ 的度数；

（2）据监测，在距离台风中心50海里范围内均会受到台风影响（假设台风在移动过程中风力保持不变）．问：在台风移动过程中，沿海城市B是否会受到台风影响？请说明理由．（参考数： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
18. 如图为一种翻盖式圆柱形茶杯，底面直径为15cm，高为20cm.

（1）如图①，小明通过按压点A打开杯盖AD注入热水（点D，D’为对应点）.若∠DAD’=120°，求点D的运动路径长.

（2）如图②，将茶杯支在桌子上，当杯底倾斜到与桌面呈53°时，恰好将热水倒出，求此时杯子最高点A距离桌面的距离.（参考数据sin53°≈0.8，cos53°≈0.6）

查看解析收藏纠错

+选题
19. 摇椅是老年人很好的休闲工具，右图是一张摇椅放在客厅的侧面示意图，摇椅静止时，以O为圆心OA为半径的弧AB的中点P着地，地面NP与弧AB相切，已知∠AOB=60°，半径OA=60cm，靠背CD与OA的夹角∠ACD=127°，C为OA的中点，CD=80cm，当摇椅沿弧AB滚动至点A着地时是摇椅向后的最大安全角度．

（精确到1cm，参考数据π取3.14，sin37°=0.60，cos37°=0.80，tan37°=0.75，sin67°=0.92，cos67°=0.39，tan67°=2.36， $\text{[math]}$ =1.41， $\text{[math]}$ =1.73）

（1）静止时靠背CD的最高点D离地面多高？

（2）静止时着地点P至少离墙壁MN的水平距离是多少时？才能使摇椅向后至最大安全角度时点D不与墙壁MN相碰．

查看解析收藏纠错

+选题
20. 在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC＝10m，拴住小狗的10m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S（m²）.

（1）如图1，画出小狗活动的区域，并求出当BC＝2m时S的值.（结果保留π）

（2）如图2，现考虑在（1）中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其他条件不变，设BC＝x，
①写出面积S与x的关系式；

②在BC的变化过程中，当S取得最小值时，求边BC的长及S的最小值.（结果保留π）

查看解析收藏纠错

+选题
21. 拓展小组研制的智能操作机器人，如图1，水平操作台为l，底座AB固定，高AB为50cm，连杆BC长度为70cm，手臂CD长度为60cm.点B，C是转动点，且AB，BC与CD始终在同一平面内，

（1）转动连杆BC，手臂CD，使 $\text{[math]}$ ， $\text{[math]}$ ，如图2，求手臂端点D离操作台 $\text{[math]}$ 的高度DE的长（精确到1cm，参考数据： $\text{[math]}$ ， $\text{[math]}$ ）.

（2）物品在操作台 $\text{[math]}$ 上，距离底座A端110cm的点M处，转动连杆BC，手臂CD，手臂端点D能否碰到点M？请说明理由.

查看解析收藏纠错

+选题
22. 为了测量学校旗杆的高度AB，数学兴趣小组带着标杆和皮尺来到操场进行测量，测量方案如下：如图，首先，小红在C处放置一平面镜，她从点C沿BC后退，当退行1.8米到D处时，恰好在镜子中看到旗杆顶点A的像，此时测得小红眼睛到地面的距离ED为1.5米；然后，小明在F 处竖立了一根高1.6米的标杆FG，发现地面上的点H、标杆顶点G和旗杆顶点A在一条直线上，此时测得FH为2.4米，DF为3.3米，已知AB⊥BH，ED⊥BH，GF⊥BH，点B、C、D、F、H在一条直线上.

（1）直接写出 $\text{[math]}$ ；

（2）请根据以上所测数据，计算学校旗杆AB的高度.

查看解析收藏纠错

+选题
23. 在几何体表面上，蚂蚁怎样爬行路径最短？

（1）如图①，圆锥的母线长为 $\text{[math]}$ ，B为母线 $\text{[math]}$ 的中点，点A在底面圆周上， $\text{[math]}$ 的长为 $\text{[math]}$ .在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径，并标出它的长（结果保留根号）.

（2）图③中的几何体由底面半径相同的圆锥和圆柱组成.O是圆锥的顶点，点A在圆柱的底面圆周上.设圆锥的母线长为l，圆柱的高为h.
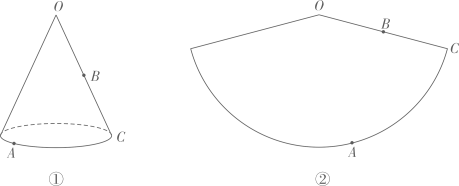
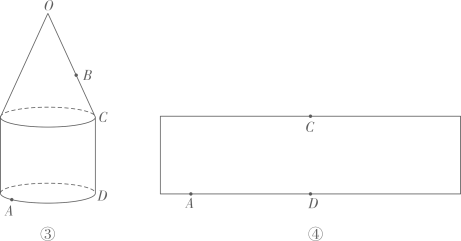
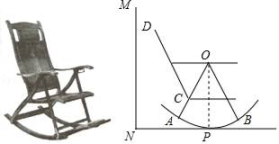
①蚂蚁从点A爬行到点O的最短路径的长为 ▲ （用含l，h的代数式表示）.

②设 $\text{[math]}$ 的长为a，点B在母线 $\text{[math]}$ 上， $\text{[math]}$ .圆柱的侧面展开图如图④所示，在图中画出蚂蚁从点A爬行到点B的最短路径的示意图，并写出求最短路径的长的思路.

查看解析收藏纠错

+选题
24. 如图是一辆自卸式货车的示意图，矩形货厢ABCD的长AB＝4 m.卸货时，货厢绕A点处的转轴旋转，货厢底部A、B两点在垂直方向上的距离与水平距离之比记作i.A点处的转轴与后车轮转轴（点M处）的水平距离叫做安全轴距，测得该车的安全轴距为0.7 m.货厢对角线AC、BD的交点G可视为货厢的重心，测得∠ACB＝66.4°.假设该车在平地上进行卸货作业（即AN为水平线）.

（1）若i＝1： $\text{[math]}$ ，求A、B两点在垂直方向上的距离；

（2）卸货时发现，当A、G两点的水平距离小于安全轴距时，会发生车辆倾覆事故.若i＝1：1，该货车会发生上述事故吗？试说明你的理由.（参考数据：sin66.4°≈0.92，cos66.4°≈0.40，cos68.6°≈0.36，tan68.6°≈0.55）

查看解析收藏纠错

+选题