北京市2021年中考数学试卷

修改时间：2021-07-14 浏览次数：614 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 如图是某几何体的展开图，该几何体是（）

A . 长方体 B . 圆柱 C . 圆锥 D . 三棱柱

查看解析收藏纠错

+选题
2. 党的十八大以来，坚持把教育扶贫作为脱贫攻坚的优先任务． $\text{[math]}$ 年，中央财政累计投入“全面改善贫困地区义务教育薄弱学校基本办学条件”专项补助资金1692亿元，将169200000000用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上， $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 下列多边形中，内角和最大的是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 实数 $\text{[math]}$ 在数轴上的对应点的位置如图所示，下列结论中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 同时抛掷两枚质地均匀的硬币，则一枚硬币正面向上､一枚硬币反面向上的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 已知 $\text{[math]}$ ．若 $\text{[math]}$ 为整数且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 43 B . 44 C . 45 D . 46

查看解析收藏纠错

+选题
8. 如图，用绳子围成周长为 $\text{[math]}$ 的矩形，记矩形的一边长为 $\text{[math]}$ ，它的邻边长为 $\text{[math]}$ ，矩形的面积为 $\text{[math]}$ ．当 $\text{[math]}$ 在一定范围内变化时， $\text{[math]}$ 和 $\text{[math]}$ 都随 $\text{[math]}$ 的变化而变化，则 $\text{[math]}$ 与 $\text{[math]}$ 与 $\text{[math]}$ 满足的函数关系分别是（）

A . 一次函数关系，二次函数关系 B . 反比例函数关系，二次函数关系 C . 一次函数关系，反比例函数关系 D . 反比例函数关系，一次函数关系

查看解析收藏纠错

+选题

二、填空题

9. 若 $\text{[math]}$ 在实数范围内有意义，则实数 $\text{[math]}$ 的取值范围是．

查看解析收藏纠错

+选题
10. 分解因式： $\text{[math]}$ ．

查看解析收藏纠错

+选题
11. 方程 $\text{[math]}$ 的解为．

查看解析收藏纠错

+选题
12. 在平面直角坐标系 $\text{[math]}$ 中，若反比例函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ 和点 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题
13. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的切线， $\text{[math]}$ 是切点．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
14. 如图，在矩形 $\text{[math]}$ 中，点 $\text{[math]}$ 分别在 $\text{[math]}$ 上， $\text{[math]}$ ．只需添加一个条件即可证明四边形 $\text{[math]}$ 是菱形，这个条件可以是（写出一个即可）．

查看解析收藏纠错

+选题
15. 有甲､乙两组数据，如表所示：

甲

11

12

13

14

15

乙

12

12

13

14

14

甲､乙两组数据的方差分别为 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ （填“＞”，“＜”或“＝”）．

查看解析收藏纠错

+选题
16. 某企业有 $\text{[math]}$ 两条加工相同原材料的生产线．在一天内， $\text{[math]}$ 生产线共加工 $\text{[math]}$ 吨原材料，加工时间为 $\text{[math]}$ 小时；在一天内， $\text{[math]}$ 生产线共加工 $\text{[math]}$ 吨原材料，加工时间为 $\text{[math]}$ 小时．第一天，该企业将5吨原材料分配到 $\text{[math]}$ 两条生产线，两条生产线都在一天内完成了加工，且加工时间相同，则分配到 $\text{[math]}$ 生产线的吨数与分配到 $\text{[math]}$ 生产线的吨数的比为．第二天开工前，该企业按第一天的分配结果分配了5吨原材料后，又给 $\text{[math]}$ 生产线分配了 $\text{[math]}$ 吨原材料，给 $\text{[math]}$ 生产线分配了 $\text{[math]}$ 吨原材料．若两条生产线都能在一天内加工完各自分配到的所有原材料，且加工时间相同，则 $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题

三、解答题

17. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
18. 解不等式组： $\text{[math]}$

查看解析收藏纠错

+选题
19. 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
20. 《淮南子･天文训》中记载了一种确定东西方向的方法，大意是：日出时，在地面上点 $\text{[math]}$ 处立一根杆，在地面上沿着杆的影子的方向取一点 $\text{[math]}$ ，使 $\text{[math]}$ 两点间的距离为10步（步是古代的一种长度单位），在点 $\text{[math]}$ 处立一根杆；日落时，在地面上沿着点 $\text{[math]}$ 处的杆的影子的方向取一点 $\text{[math]}$ ，使 $\text{[math]}$ 两点间的距离为10步，在点 $\text{[math]}$ 处立一根杆．取 $\text{[math]}$ 的中点 $\text{[math]}$ ，那么直线 $\text{[math]}$ 表示的方向为东西方向．

（1）上述方法中，杆在地面上的影子所在直线及点 $\text{[math]}$ 的位置如图所示．使用直尺和圆规，在图中作 $\text{[math]}$ 的中点 $\text{[math]}$ （保留作图痕迹）；

（2）在如图中，确定了直线 $\text{[math]}$ 表示的方向为东西方向．根据南北方向与东西方向互相垂直，可以判断直线 $\text{[math]}$ 表示的方向为南北方向，完成如下证明．
证明：在 $\text{[math]}$ 中， $\text{[math]}$ ▲ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，

$\text{[math]}$ ▲ （填推理的依据）．

∵直线 $\text{[math]}$ 表示的方向为东西方向，

∴直线 $\text{[math]}$ 表示的方向为南北方向．

查看解析收藏纠错

+选题
21. 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ ．

（1）求证：该方程总有两个实数根；

（2）若 $\text{[math]}$ ，且该方程的两个实数根的差为2，求 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
22. 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ，垂足为 $\text{[math]}$ ．

（1）求证：四边形 $\text{[math]}$ 是平行四边形；

（2）若 $\text{[math]}$ 平分 $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
23. 在平面直角坐标系 $\text{[math]}$ 中，一次函数 $\text{[math]}$ 的图象由函数 $\text{[math]}$ 的图象向下平移1个单位长度得到．

（1）求这个一次函数的解析式；

（2）当 $\text{[math]}$ 时，对于 $\text{[math]}$ 的每一个值，函数 $\text{[math]}$ 的值大于一次函数 $\text{[math]}$ 的值，直接写出 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题
24. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ 于点 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ ；

（2）连接 $\text{[math]}$ 并延长，交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．若 $\text{[math]}$ 的半径为5， $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
25. 为了解甲､乙两座城市的邮政企业4月份收入的情况，从这两座城市的邮政企业中，各随机抽取了25家邮政企业，获得了它们4月份收入（单位：百万元）的数据，并对数据进行整理､描述和分析．下面给出了部分信息．
$\text{[math]}$ ．甲城市邮政企业4月份收入的数据的频数分布直方图如下（数据分成5组： $\text{[math]}$ ）：

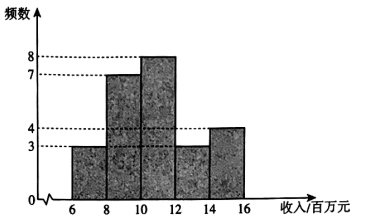
$\text{[math]}$ ．甲城市邮政企业4月份收入的数据在 $\text{[math]}$ 这一组的是：10.0，10.0，10.1，10.9，11.4，11.5，11.6，11.8

$\text{[math]}$ ．甲､乙两座城市邮政企业4月份收入的数据的平均数､中位数如下：

平均数

中位数

甲城市

10.8

$\text{[math]}$

乙城市

11.0

11.5

根据以上信息，回答下列问题：

（1）写出表中 $\text{[math]}$ 的值；

（2）在甲城市抽取的邮政企业中，记4月份收入高于它们的平均收入的邮政企业的个数为 $\text{[math]}$ ．在乙城市抽取的邮政企业中，记4月份收入高于它们的平均收入的邮政企业的个数为 $\text{[math]}$ ．比较 $\text{[math]}$ 的大小，并说明理由；

（3）若乙城市共有200家邮政企业，估计乙城市的邮政企业4月份的总收入（直接写出结果）．

查看解析收藏纠错

+选题
26. 在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ 和点 $\text{[math]}$ 在抛物线 $\text{[math]}$ 上．

（1）若 $\text{[math]}$ ，求该抛物线的对称轴；

（2）已知点 $\text{[math]}$ 在该抛物线上．若 $\text{[math]}$ ，比较 $\text{[math]}$ 的大小，并说明理由．

查看解析收藏纠错

+选题
27. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的中点，点 $\text{[math]}$ 在 $\text{[math]}$ 上，以点 $\text{[math]}$ 为中心，将线段 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，连接 $\text{[math]}$ ．

（1）比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小；用等式表示线段 $\text{[math]}$ 之间的数量关系，并证明；

（2）过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，交 $\text{[math]}$ 于点 $\text{[math]}$ ，用等式表示线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并证明．

查看解析收藏纠错

+选题
28. 在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ 的半径为1，对于点 $\text{[math]}$ 和线段 $\text{[math]}$ ，给出如下定义：若将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转可以得到 $\text{[math]}$ 的弦 $\text{[math]}$ （ $\text{[math]}$ 分别是 $\text{[math]}$ 的对应点），则称线段 $\text{[math]}$ 是 $\text{[math]}$ 的以点 $\text{[math]}$ 为中心的“关联线段”．

（1）如图，点 $\text{[math]}$ 的横､纵坐标都是整数．在线段 $\text{[math]}$ 中， $\text{[math]}$ 的以点 $\text{[math]}$ 为中心的“关联线段”是；

（2） $\text{[math]}$ 是边长为1的等边三角形，点 $\text{[math]}$ ，其中 $\text{[math]}$ ．若 $\text{[math]}$ 是 $\text{[math]}$ 的以点 $\text{[math]}$ 为中心的“关联线段”，求 $\text{[math]}$ 的值；

（3）在 $\text{[math]}$ 中， $\text{[math]}$ ．若 $\text{[math]}$ 是 $\text{[math]}$ 的以点 $\text{[math]}$ 为中心的“关联线段”，直接写出 $\text{[math]}$ 的最小值和最大值，以及相应的 $\text{[math]}$ 长．

查看解析收藏纠错

+选题

	平均数	中位数
甲城市	10.8	$\text{[math]}$
乙城市	11.0	11.5

甲	11	12	13	14	15
乙	12	12	13	14	14

北京市2021年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨