山东省青岛市李沧区2021年中考数学二模试卷

1. 下列电视台的台标，是中心对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
2. 下列选项中，对 $\text{[math]}$ 的说法错误的是（）．

A . $\text{[math]}$ 的相反数是 $\text{[math]}$ B . $\text{[math]}$ 的倒数是 $\text{[math]}$ C . $\text{[math]}$ 的绝对值是 $\text{[math]}$ D . $\text{[math]}$ 是有理数

查看解析收藏纠错

+选题
3. 某中学在芦山地震捐款活动中，共捐款二十一万三千元．这一数据用科学记数法表示为（）

A . $\text{[math]}$ 元 B . $\text{[math]}$ 元 C . $\text{[math]}$ 元 D . $\text{[math]}$ 元

查看解析收藏纠错

+选题
4. 如图是一个几何体的三视图，则这个几何体是（）．

A . 三棱锥 B . 圆锥 C . 三棱柱 D . 圆柱

查看解析收藏纠错

+选题
5. 一次数学测试后，某小组五名同学的成绩及数据分析如下表所示（有两个数据被遮盖），那么被遮盖的两个数据依次是（）．

甲

乙

丙

丁

戊

方差

平均成绩

81

79

■

80

82

■

80

A . 78， $\text{[math]}$ B . 78，2 C . 80， $\text{[math]}$ D . 80，2

查看解析收藏纠错

+选题
6. 下列运算正确的是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，△ABC内接于⊙O，∠A＝50°.E是边BC的中点，连接OE并延长，交⊙O于点D，连接BD，则∠D的大小为（）

A . 55° B . 65° C . 60° D . 75°

查看解析收藏纠错

+选题
8. 二次函数 $\text{[math]}$ 的顶点坐标为（-1，n），其部分图象如图所示．以下结论错误的是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 关于 $\text{[math]}$ 的方程 $\text{[math]}$ 无实数根

查看解析收藏纠错

+选题

9. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
10. 为改善生态环境，防止水土流失，某村计划在荒坡上种1000棵树．由于青年志愿者的支援，每天比原计划多种25%，结果提前5天完成任务，则该村原计划每天种树棵．

查看解析收藏纠错

+选题
11.
如图，D是△ABC内一点，BD⊥CD，AD=6，BD=4，CD=3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是

查看解析收藏纠错

+选题
12. 如图，正方形 $\text{[math]}$ 的边长为2，点 $\text{[math]}$ 在 $\text{[math]}$ 轴的正半轴上，点 $\text{[math]}$ 在 $\text{[math]}$ 轴的负半轴上，将正方形 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转30°至正方形 $\text{[math]}$ 的位置， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为．

查看解析收藏纠错

+选题
13. 如图，以等边三角形 $\text{[math]}$ 的 $\text{[math]}$ 边为直径画半圆，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是圆的切线，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线交 $\text{[math]}$ 于点 $\text{[math]}$ ．若 $\text{[math]}$ 的长为2，则 $\text{[math]}$ 的长为．

查看解析收藏纠错

+选题
14. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，当点 $\text{[math]}$ 的对应点 $\text{[math]}$ 落在线段 $\text{[math]}$ 的垂直平分线上时， $\text{[math]}$ 的长等于.

查看解析收藏纠错

+选题

15. 已知：如图，四边形 $\text{[math]}$ ．
求作：点 $\text{[math]}$ ，使点 $\text{[math]}$ 在四边形 $\text{[math]}$ 内部， $\text{[math]}$ ，并且点 $\text{[math]}$ 到 $\text{[math]}$ 两边的距离相等．

查看解析收藏纠错

+选题
16.

（1）化简： $\text{[math]}$ ；

（2）解不等式组： $\text{[math]}$ ．

查看解析收藏纠错

+选题

17. 某校有2000名学生，为了解全校学生的上学方式，该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查．整理样本数据，得到下列图表：

某校150名学生上学方式频数分布表

方式	划记	频数
步行	正正正	15
骑车	正正正正正正正正正正一	51
乘公共交通工具	正正正正正正正正正	45
乘私家车	正正正正正正	30
其它	正	9
合计		150

（1）理解画线语句的含义，回答问题：如果150名学生全部在同一个年级抽取，这样的抽样是否合理？请说明理由；

（2）根据抽样调查的结果，将估计出的全校2000名学生上学方式的情况绘制成条形统计图；

（3）该校数学兴趣小组结合调查获取的信息，向学校提出了一些建议．如：骑车上学的学生数约占全校的34%，建议学校合理安排自行车停车场地．请你结合上述统计的全过程，再提出一条合理化建议．

查看解析收藏纠错

+选题

18. 某中学举行“中国梦•我的梦”演讲比赛．九年级（1）班的小明和小刚都想参加．现设计了如下游戏规则：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去；否则小刚去，这个游戏规则是否公平？并说明理由．

查看解析收藏纠错

+选题

19. 图①是甘肃省博物馆的镇馆之宝——铜奔马，又称“马踏飞燕”，于1969年10月出土于武威市的雷台汉墓，1983年10月被国家旅游局确定为中国旅游标志，在很多旅游城市的广场上都有“马踏飞燕”雕塑，某学习小组把测量本城市广场的“马踏飞燕”雕塑（图②）最高点离地面的高度作为一次课题活动，同学们制定了测量方案，并完成了实地测量，测得结果如下表：

课题	测量“马踏飞燕”雕塑最高点离地面的高度
测量示意图			如图，雕塑的最高点B到地面的高度为 $\text{[math]}$ ，在测点C用仪器测得点B的仰角为 $\text{[math]}$ ，前进一段距离到达测点E，再用该仪器测得点B的仰角为 $\text{[math]}$ ，且点A，B，C，D，E，F均在同一竖直平面内，点A，C，E在同一条直线上.
测量数据	$\text{[math]}$ 的度数	$\text{[math]}$ 的度数	$\text{[math]}$ 的长度	仪器 $\text{[math]}$ （ $\text{[math]}$ ）的高度
测量数据	$\text{[math]}$	$\text{[math]}$	5米	$\text{[math]}$ 米

请你根据上表中的测量数据，帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度（结果保留一位小数）.（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题

20. 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 在第一象限的图象交于 $\text{[math]}$ 和B两点，与x轴交于点C ．

（1）求反比例函数的解析式；

（2）若点P在x轴上，且 $\text{[math]}$ 的面积为5，求点P的坐标．

查看解析收藏纠错

+选题
21. 如图，在 $\text{[math]}$ 与 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ．过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ ≌ $\text{[math]}$ ；

（2）若 $\text{[math]}$ ，四边形 $\text{[math]}$ 是什么特殊四边形？请说明理由．

查看解析收藏纠错

+选题

22. 某商店销售一种商品，经市场调查发现：该商品的周销售量 $\text{[math]}$ （件）是售价 $\text{[math]}$ （元/件）的一次函数，其售价、周销售量、周销售利润 $\text{[math]}$ （元）的三组对应值如表：

售价 $\text{[math]}$ （元/件）	50	60	80
周销售量 $\text{[math]}$ （件）	100	80	40
周销售利润 $\text{[math]}$ （元）	1000	1600	1600

注：周销售利润＝周销售量×（售价-进价）

（1）求当售价是多少元/件时，周销售利润最大；

（2）由于某种原因，该商品进价提高了 $\text{[math]}$ 元/件 $\text{[math]}$ ，物价部门规定该商品售价不得超过65元/件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系．若周销售最大利润是1400元，求 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题

23. （问题）用n边形的对角线把n边形分割成（n-2个三角形，共有多少种不同的分割方案 $\text{[math]}$ ？
（探究）为了解决上面的数学问题，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进转化，最后猜想得出结论．不妨假设n边形的分割方案有 $\text{[math]}$ 种．

探究一：用四边形的对角线把四边形分割成2个三角形，共有多少种不同的分割方案？如图①，图②，显然，只有2种不同的分割方案．所以， $\text{[math]}$ ．

探究二：用五边形的对角线把五边形分割成3个三角形，共有多少种不同的分割方案？不妨把分割方案分成三类：

第1类：如图③，用点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 连接，先把五边形分割转化成1个三角形和1个四边形，再把四边形分割成2个三角形，由探究一知，有 $\text{[math]}$ 种不同的分割方案，所以，此类共有 $\text{[math]}$ 种不同的分割方案．

第2类：如图④，用点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 连接，把五边形分割成3个三角形，有1种不同的分割方案，可视为 $\text{[math]}$ 种分割方案．

第3类：如图⑤，用点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 连接，先把五边形分割转化成1个三角形和1个四边形，再把四边形分割成2个三角形，由探究一知，有f（4）种不同的分割方案，所以，此类共有f（4）种不同的分割方案．

所以， $\text{[math]}$ （种）

探究三：用六边形的对角线把六边形分割成4个三角形，共有多少种不同的分割方案？不妨把分割方案分成四类：

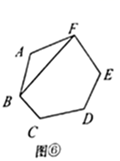
第1类：如图⑥，用 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 连接，先把六边形分割转化成1个三角形和1个五边形，再把五边形分割成3个三角形，由探究二知，有 $\text{[math]}$ 种不同的分割方案，所以，此类共有 $\text{[math]}$ 种不同的分割方案．

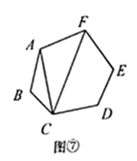
第2类：如图⑦，用 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 连接，先把六边形分割转化成2个三角形和1个四边形．再把四边形分割成2个三角形，由探究一知，有 $\text{[math]}$ 种不同的分割方案．所以，此类共有 $\text{[math]}$ 种分割方案．

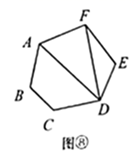
第3类：如图⑧，用 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 连接，先把六边形分割转化成2个三角形和1个四边形．再把四边形分割成2个三角形，由探究一知，有 $\text{[math]}$ 种不同的分割方案．所以，此类共有 $\text{[math]}$ 种分割方案．

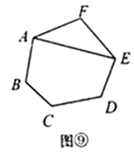
第4类：如图，用 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 连接，先把六边形分割转化成1个三角形和1个五边形，再把五边形分割成3个三角形，由探究二知，有 $\text{[math]}$ 种不同的分割方案．所以，此类共有 $\text{[math]}$ 种分割方案．

所以， $\text{[math]}$

$\text{[math]}$ （种）

探究四：用七边形的对角线把七边形分割成5个三角形，则 $\text{[math]}$ 与 $\text{[math]}$ 的关系为 $\text{[math]}$ ，共有种不同的分割方案．

……

（结论）用 $\text{[math]}$ 边形的对角线把 $\text{[math]}$ 边形分割成 $\text{[math]}$ 个三角形，共有多少种不同的分割方案 $\text{[math]}$ ？（直接写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的关系式，不写解答过程）

（应用）用九边形的对角线把九边形分割成7个三角形，共有多少种不同的分割方案？（应用上述结论中的关系式求解）

查看解析收藏纠错

+选题
24. 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的一点， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边的中点，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿边 $\text{[math]}$ 以 $\text{[math]}$ 的速度向终点 $\text{[math]}$ 运动，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，设动点 $\text{[math]}$ 的运动时间是 $\text{[math]}$ ．

（1）求 $\text{[math]}$ 为何值时， $\text{[math]}$ ？

（2）设 $\text{[math]}$ 的面积为 $\text{[math]}$ ，写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；

（3）当 $\text{[math]}$ 平分四边形 $\text{[math]}$ 的面积时，求 $\text{[math]}$ 的值；

（4）是否存在时刻 $\text{[math]}$ ，使得点 $\text{[math]}$ 关于 $\text{[math]}$ 的对称点 $\text{[math]}$ ，落在线段 $\text{[math]}$ 上，若存在，求出 $\text{[math]}$ 值，若不存在，说明理由．

查看解析收藏纠错

+选题

山东省青岛市李沧区2021年中考数学二模试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

甲	乙	丙	丁	戊	方差	平均成绩
81	79	■	80	82	■	80

山东省青岛市李沧区2021年中考数学二模试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨