注册

题型：单选题题类：常考题难易度：容易

高中数学人教版选修1-2（文科）第一章统计案例 1.1 回归分析的基本思想及其初步应用

某考察团对全国10大城市进行职工人均工资水平x（千元）与居民人均消费水平y（千元）进行统计调查，y与x具有相关关系，回归方程为 $\text{[math]}$ ＝0.66x＋1.562.若某城市居民人均消费水平为7.675千元，估计该城市人均消费额占人均工资收入的百分比约为（）

A、83% B、72% C、67% D、66%

举一反三

在线性回归模型y=bx+a+e中，下列说法正确的是（　　）

在一段时间内，某种商品的价格x(元)和需求量y(件)之间的一组数据如下表所示：

价格x/元	14	16	18	20	22
需求量y/件	56	50	43	41	37

求出y关于x的线性回归方程，并说明拟合效果的好坏．

(参考数据： $\text{[math]}$ )

某互联网公司为了确定下一季度的前期广告投入计划，收集了近 $\text{[math]}$ 个月广告投入量 $\text{[math]}$ （单位：万元）和收益 $\text{[math]}$ （单位：万元）的数据如下表：

月份	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
广告投入量	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
收益	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

他们分别用两种模型① $\text{[math]}$ ，② $\text{[math]}$ 分别进行拟合，得到相应的回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值：

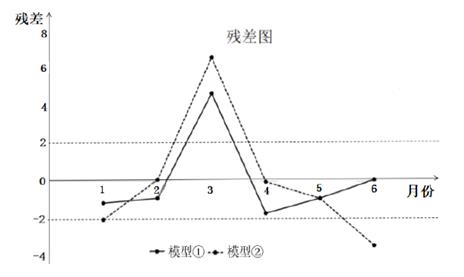
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

（Ⅰ）根据残差图，比较模型①，②的拟合效果，应选择哪个模型？并说明理由；

（Ⅱ）残差绝对值大于 $\text{[math]}$ 的数据被认为是异常数据，需要剔除：

（ⅰ）剔除异常数据后求出（Ⅰ）中所选模型的回归方程；

（ⅱ）若广告投入量 $\text{[math]}$ 时，该模型收益的预报值是多少？

附：对于一组数据 $\text{[math]}$ ， $\text{[math]}$ ，……， $\text{[math]}$ ，其回归直线 $\text{[math]}$ 的斜率和截距的最小二乘估计分别为：

 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ .

2019年5月5日6时许，桂林市雁山区一出租房发生一起重大火灾，事故发生后，附近消防员及时赶到，控制住火情，将灾难损失降到了最低．某保险公司统计的数据表明：居民住宅区到最近消防站的距离 $\text{[math]}$ (单位：千米)和火灾所造成的损失数额 $\text{[math]}$ (单位：千元)有如下的统计资料：

距消防站距离 $\text{[math]}$ （千米）	1.8	2.6	3.1	4.3	5.5	6.1
火灾损失费用 $\text{[math]}$ （千元）	17.8	19.6	27.5	31.3	36.0	43.2

如果统计资料表明 $\text{[math]}$ 与 $\text{[math]}$ 有线性相关关系，试求(解答过程中，各种数据都精确到0.01)

（I）相关系数 $\text{[math]}$ ；

（Ⅱ）线性回归方程；

（Ⅲ）若发生火灾的某居民区与最近的消防站相距10.0千米，评估一下火灾的损失．

参考数据： $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

参考公式：相关系数 $\text{[math]}$

回归方程 $\text{[math]}$ 中斜率和截距的最小二乘法估计公式分别为： $\text{[math]}$ ， $\text{[math]}$ ．

在一段时间内，分5次测得某种商品的价格 $\text{[math]}$ （万元）和需求量 $\text{[math]}$ 之间的一组数据为：

	1	2	3	4	5
价格 $\text{[math]}$	1.4	1.6	1.8	2	2.2
需求量 $\text{[math]}$	12	10	7	5	3

已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，

某公司根据近几年经营经验，得到广告支出与获得利润数据如下：

广告支出x/万元	2	5	8	11	15	19
利润y/万元	33	45	50	53	58	64

根据表中数据可得利润y关于广告支出x的经验回归方程为 $\text{[math]}$ ．据此经验回归方程，若计划利润达到100万元，估计需要支出广告费（）

返回首页

相关试卷

试题篮

公司介绍

Company Introduction

服务介绍

Service Introduction

帮助中心

Help center

二一教育APP

二一教育APP

400-637-9991

周一至周五 8:30-17:30

在线咨询客服