注册

题型：解答题题类：模拟题难易度：普通

新疆乌鲁木齐地区2019届高三理数第二次质量监测试卷

某互联网公司为了确定下一季度的前期广告投入计划，收集了近 $\text{[math]}$ 个月广告投入量 $\text{[math]}$ （单位：万元）和收益 $\text{[math]}$ （单位：万元）的数据如下表：

月份	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
广告投入量	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
收益	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

他们分别用两种模型① $\text{[math]}$ ，② $\text{[math]}$ 分别进行拟合，得到相应的回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值：

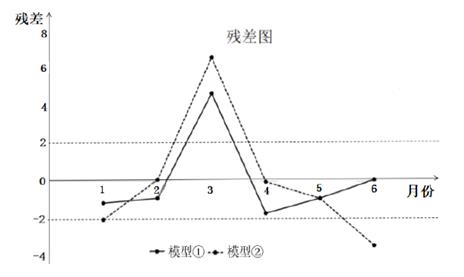
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

（Ⅰ）根据残差图，比较模型①，②的拟合效果，应选择哪个模型？并说明理由；

（Ⅱ）残差绝对值大于 $\text{[math]}$ 的数据被认为是异常数据，需要剔除：

（ⅰ）剔除异常数据后求出（Ⅰ）中所选模型的回归方程；

（ⅱ）若广告投入量 $\text{[math]}$ 时，该模型收益的预报值是多少？

附：对于一组数据 $\text{[math]}$ ， $\text{[math]}$ ，……， $\text{[math]}$ ，其回归直线 $\text{[math]}$ 的斜率和截距的最小二乘估计分别为：

 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ .

举一反三

某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：

日期	1月10日	2月10日	3月10日	4月10日	5月10日	6月10日
昼夜温差x（℃）	10	11	13	12	8	6
就诊人数y（人）	22	25	29	26	16	12

该兴趣小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验．

（Ⅰ）求选取的2组数据恰好是相邻两个月的概率；

（Ⅱ）若选取的是1月与6月的两组数据，请根据2至5月份的数据，求出y关于x的线性回归方程y=bx+a；

（Ⅲ）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想？

某同学在求解某回归方程中，已知x，y的取值结果（y与x呈线性相关）如表：

x	2	3	4
y	6	4	m

并且求得了线性回归方程为 $\text{[math]}$ =﹣ $\text{[math]}$ x+ $\text{[math]}$ ，则m等于{#blank#}1{#/blank#}．

为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度x（单位：cm）满足关系：C（x）= $\text{[math]}$ （0≤x≤10），若不建隔热层，每年能源消耗费用为8万元．设f（x）为隔热层建造费用与20年的能源消耗费用之和．

某单位有员工1000名，平均每人每年创造利润10万元．为了增加企业竞争力，决定优化产业结构，调整出x（x∈N^*）名员工从事第三产业，调整后他们平均每人每年创造利润为10（a﹣ $\text{[math]}$ ）万元（a＞0），剩下的员工平均每人每年创造的利润为原来（1+ $\text{[math]}$ ）倍．

登山族为了了解某山高y（km）与气温x（℃）之间的关系，随机统计了4次山高与相应的气温，并制作了对照表如下：

气温（℃）	18	13	10	﹣1
山高（km）	24	34	38	64

由表中数据，得到线性回归方程 $\text{[math]}$ =﹣2x+ $\text{[math]}$ （ $\text{[math]}$ ∈R），由此估计山高为72km处气温的度数是（）

已知函数 $\text{[math]}$ 的定义域为 $\text{[math]}$ ，值域为 $\text{[math]}$ ，即 $\text{[math]}$ ，若 $\text{[math]}$ ，则称 $\text{[math]}$ 在 $\text{[math]}$ 上封闭.

返回首页

相关试卷

试题篮

公司介绍

Company Introduction

服务介绍

Service Introduction

帮助中心

Help center

二一教育APP

二一教育APP

400-637-9991

周一至周五 8:30-17:30

在线咨询客服