题型:综合题 题类:常考题 难易度:普通
山西省吕梁市文水县2019-2020学年七年级下学期数学期末试卷
问题情境
在综合实践课上,老师组织七年级(2)班的同学开展了探究两角之间数量关系的数学活动,如图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
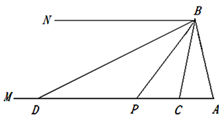
“快乐小组”经过探索后发现:
当∠A=60º时,∠CBD=∠A.请说明理由.
“智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变,请写出它们的关系,并说明理由.
试题篮