- 二一组卷

题型：综合题题类：模拟题难易度：普通

甘肃省兰州市2019届九年级中考适应性考试数学试卷（二）

某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整.

【收集数据】

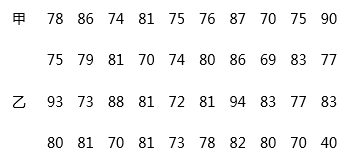
从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如下：

【整理、描述数据】

按如下分数段整理、描述这两组样本数据：

成绩 $\text{[math]}$

人数

部门

40≤x≤49

50≤x≤59

60≤x≤69

70≤x≤79

80≤x≤89

90≤x≤100

甲

乙

（说明：成绩80分及以上为生产技能优秀，70--79分为生产技能良好，60--69分为生产技能合格，60分以下为生产技能不合格）

【分析数据】

两组样本数据的平均数、中位数、众数如下表所示：

部门	平均数	中位数	众数
甲	78.3	77.5	75
乙	78	80.5	81

【得出结论】

$\text{[math]}$ .估计乙部门生产技能优秀的员工人数为；

$\text{[math]}$ .可以推断出部门员工的生产技能水平较高，理由为.（至少从两个不同的角度说明推断的合理性）

举一反三

如果将所给定的数据组中的每个数都减去一个非零常数，那么该数组的（）

为参加2018年“宜宾市初中毕业生升学体育考试”，小聪同学每天进行立定跳远练习，并记录下其中7天的最好成绩（单位：m）分别为：2.21，2.12，2.43，2.39，2.43，2.40，2.43．这组数据的中位数和众数分别是{#blank#}1{#/blank#}．

甲、乙两名同学分别进行6次射击训练，训练成绩（单位：环）如下表

	第一次	第二次	第三次	第四次	第五次	第六交
甲	9	8	6	7	8	10
乙	8	7	9	7	8	8

对他们的训练成绩作如下分析，其中说法正确的是（）

下列说法中正确的是（）

某校为了选拔一名百米赛跑运动员参加市中学生运动会，组织了 $\text{[math]}$ 次预选赛，其中甲，乙两名运动员较为突出，他们在 $\text{[math]}$ 次预选赛中的成绩（单位：秒）如下表所示：

甲	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
乙	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

由于甲，乙两名运动员的成绩的平均数相同，学校决定依据他们成绩的稳定性进行选拔，那么被选中的运动员是{#blank#}1{#/blank#}．

巴黎奥运会男子50米步枪三姿决赛于当地时间8月1日上午结束，中国运动员刘宇坤不负众望，最终夺冠，小宇观看了比赛的直播，并记录和分析了比赛数据，得到如下信息：

a．决赛共有8名选手参加，先后进行跪姿、卧姿、立姿三种姿势的射击，具体规则为：

·每位选手先进行40发子弹的基础射击（依次为跪姿15发、卧姿15发、立姿10发），按选手所获得的总环数从高到低依次排名；

·在基础射击环节结束后，排名最后两位的选手被淘汰，其余选手进行单发淘汰赛，淘汰赛为立姿，每轮射击1发子弹后，淘汰赛与基础射击总环数之和最低的1名选手被淘汰，直到5轮淘汰后最终决出冠军；

·在淘汰赛进行过程中，当排名最后的若干位选手总环数相同时，将进行加枪决胜，加枪的环数不计入总环数中；

·选手每一次射击的环数最低为 $\text{[math]}$ ，最高为 $\text{[math]}$ ，且均为 $\text{[math]}$ 的整数倍．

b．基础射击结束后8名选手的三种姿势平均成绩如下表所示

选手	A	B	C	D	E	F	G	H
跪姿（15发）	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
卧姿（15发）	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
立姿（10发）	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
是否淘汰			淘汰					淘汰

c．决赛结束后，最终获得前三名的选手恰好是基础射击中立姿平均成绩排名前三的选手，且他们最终的排名顺序与他们跪姿的排名顺序一致．这三人单发淘汰赛的成绩如下表所示

决赛排名	第1轮	第2轮	第3轮	第4轮	第5轮
1	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	m	$\text{[math]}$
2	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
3	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	——

d．中国选手刘宇坤在决赛中全部15发立姿射击的总环数为 $\text{[math]}$ 环．

根据上述信息回答：

相关试卷

公司介绍

服务介绍

帮助中心