题型：综合题 题类：压轴题 难易度：普通
新华师大版数学八年级上册第十二章第一节12.1.1同底数幂的乘法同步练习
材料：一般地，n个相同的因数a相乘：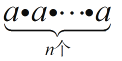 
记为an ．
如23=8，此时，3叫做以2为底8的对数，记为log28（即log28=3）．
一般地，若an=b（a＞0且a≠1，b＞0），则n叫做以a为底b的对数，记为logab（即logab=n）．如34=81，则4叫做以3为底81的对数，记为log381（即log381=4）．
问题：
|
加数的个数n |
连续偶数的和S |
|
1 |
2=1×2 |
|
2 |
2+4=6=2×3 |
|
3 |
2+4+6=12=3×4 |
|
4 |
2+4+6+8=20=4×5 |
|
5 |
2+4+6+8+10=30=5×6 |
试题篮
