浙江省宁波市鄞州实验中学2018届九年级下学期数学3月联考试卷

修改时间：2024-07-13 浏览次数：567 类型：月考试卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题：

1. 计算 $\text{[math]}$ 的结果是（）

A . -7 B . -1 C . 1 D . 7

查看解析收藏纠错

+选题
2. 10045用科学记数法表示为 ( ）

A . 10.045× 10³ B . 1.0045×10³ C . 1.0045×10⁴ D . 0.10045×10⁵

查看解析收藏纠错

+选题
3. 如图所示的支架是由两个长方体构成的组合体，则它的主视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 下列运算，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是（）

A . x=0 B . x=4 C . x≠0 D . x≠4

查看解析收藏纠错

+选题
6. 剪纸是中国特有的民间艺术，在如图所示的四个剪纸图案中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
7. 某区10名学生参加市级汉字听写大赛，他们得分情况如下表：
人数
3
4
2
1
分数
80
85
90
95
那么这10名学生所得分数的平均数和众数分别是（）

A . 85和82.5 B . 85.5和85 C . 85和85 D . 85.5和80

查看解析收藏纠错

+选题
8. 如图，在 $\text{[math]}$ 中，点D，E分别在边AB，AC上， $\text{[math]}$ ．已知DE=6， $\text{[math]}$ ，那么BC的长是（）

A . 4.5 B . 8 C . 10.5 D . 14

查看解析收藏纠错

+选题
9. 关于x的二次函数y=a（x+1）（x﹣m），其图象的对称轴在y轴的右侧，则实数a、m应满足（　　）

A . a＞0，m＜﹣1 B . a＞0，m＞1 C . a≠0，0＜m＜1 D . a≠0，m＞1

查看解析收藏纠错

+选题
10. 如图，在▱ABCD中，AD＝2，AB＝4，∠A＝30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是（）

A . 3－ $\text{[math]}$ B . 3－ $\text{[math]}$ C . 4－ $\text{[math]}$ D . 4－ $\text{[math]}$

查看解析收藏纠错

+选题
11. 如图，直线y＝ $\text{[math]}$ x与双曲线y＝ $\text{[math]}$ （k>0，x>0）交于点A，将直线y＝ $\text{[math]}$ x向上平移4个单位长度后，与y轴交于点C，与双曲线y＝ $\text{[math]}$ （k>0，x>0）交于点B，若OA＝3BC，则k的值为（）

A . 3 B . 6 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
12. 某班有20位同学参加围棋、象棋比赛，甲说：“只参加一项的人数大于14人” ；乙说：“两项都参加的人数小于5人” .对于甲、乙两人的说法，有下列四个命题，其中真命题的是（）

A . 若甲对，则乙对 B . .若乙对，则甲对 C . 若乙错，则甲错 D . 若甲错，则乙对

查看解析收藏纠错

+选题

二、填空题

13. 分解因式：x²－4＝.

查看解析收藏纠错

+选题
14. 一个不透明的袋子中有2个红球、3个黄球和4个蓝球，这些球除颜色外完全相同，从袋子中随机摸出一个球，它是红色球的概率为．

查看解析收藏纠错

+选题
15. 如图①，小敏利用课余时间制作了一个脸盆架，图②是它的截面图，垂直放置的脸盆与架子的交点为A，B，AB＝48cm，脸盆的最低点C到AB的距离为12 cm，则该脸盆的半径为cm.

查看解析收藏纠错

+选题
16. 如图，在△ABC中，AB＝2，AC＝ $\text{[math]}$ ，∠BAC＝105°，△ABD，△ACE，△BCF都是等边三角形，则四边形AEFD的面积为．

查看解析收藏纠错

+选题
17. 如图，在平面直角坐标系中，0为坐标原点，点A的坐标为（－4，0），直线BC经过点B（－4，3），C（0，3），将四边形OABC绕点O按顺时针方向旋转α度（0＜α≤l80°）得到四边形OA′B′C′，此时直线OA′、直线B′C′，分别与直线BC相交于P，Q．在四边形OABC旋转过程中，若BP= $\text{[math]}$ BQ 则点P的坐标为．

查看解析收藏纠错

+选题

三、解答题

18. 按要求计算下列各题：

（1）计算：（2017－π）⁰－ $\text{[math]}$ ＋|－2|；

（2）化简： $\text{[math]}$ ÷ $\text{[math]}$ .

查看解析收藏纠错

+选题
19. 图①是小明在健身器材上进行仰卧起坐锻炼时的情景，图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图．已知AC＝0.66米，BD＝0.26米，α＝20°.(参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364)

（1）求AB的长(精确到0.01米)；

（2）若测得ON＝0.8米，试计算小明头顶由N点运动到M点的路径MN的长度．(结果保留π)

查看解析收藏纠错

+选题
20. 手工课上，老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形，聪明的你请在下列四个正方形中画出不同的裁剪线，并直接写出每种不同分割后得到的最小等腰直角三角形面积.（注：不同的分法，面积可以相等）.

查看解析收藏纠错

+选题
21. 我区积极开展“体育大课间”活动，引导学生坚持体育锻炼，某校根据实际情况，决定主要开设A：乒乓球，B：篮球，C：跑步．D：足球四种运动项目．为了解学生最喜欢哪一种项目，随机抽取了部分学生进行调査，并将调查结果绘制成如下统计图．请你结合图中信息解答下列问题：

（1）求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数；

（2）请把条形统计图补充完整；

（3）已知该校有2000人，请根据样本估计全校最喜欢足球的人数是多少？

查看解析收藏纠错

+选题
22. 如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

（1）求证：AF=DC；

（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

查看解析收藏纠错

+选题
23. 某宾馆有50个房间供游客居住，当每个房间定价120元时，房间会全部住满，当每个房间每天的定价每增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，设每个房间定价增加10x元(x为整数)．

（1）直接写出每天游客居住的房间数量y与x的函数关系式；

（2）设宾馆每天的利润为W元，当每个房间定价为多少元时，宾馆每天所获利润最大，最大利润是多少？

（3）某日，宾馆了解当天的住宿情况，得到以下信息：
①当日所获利润不低于5000元，
②宾馆为游客居住的房间共支出费用没有超过600元，
③每个房间刚好住满2人．
问：这天宾馆入住的游客人数最少有多少人？

查看解析收藏纠错

+选题
24. 如图，抛物线y＝x²＋bx＋c经过B(－1，0)，D(－2，5)两点，与x轴另一交点为A，点H是线段AB上一动点，过点H的直线PQ⊥x轴，分别交直线AD、抛物线于点Q、P.

（1）求抛物线的解析式；

（2）是否存在点P，使∠APB＝90°，若存在，求出点P的横坐标，若不存在，说明理由；

（3）连接BQ，一动点M从点B出发，沿线段BQ以每秒1个单位的速度运动到Q，再沿线段QD以每秒 $\text{[math]}$ 个单位的速度运动到D后停止，当点Q的坐标是多少时，点M在整个运动过程中用时t最少？

查看解析收藏纠错

+选题
25. 如图1，点P为四边形ABCD所在平面上的点，如果∠PAD=∠PBC，则称点P为四边形ABCD关于A、B的等角点，以点C为坐标原点，BC所在直线为x轴建立平面直角坐标系，点B的横坐标为﹣6．

（1）如图2，若A、D两点的坐标分别为A（﹣6，4）、D（0，4），点P在DC边上，且点P为四边形ABCD关于A、B的等角点，则点P的坐标为；

（2）如图3，若A、D两点的坐标分别为A（﹣2，4）、D（0，4）．
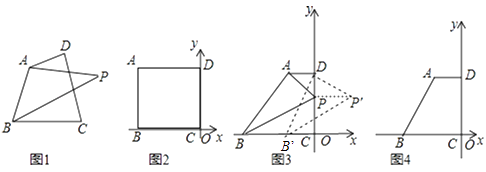
①若P在DC边上时，求四边形ABCD关于A、B的等角点P的坐标；
②在①的条件下，将PB沿x轴向右平移m个单位长度（0＜m＜6）得到线段P′B′，连接P′D，B′D，试用含m的式子表示P′D²+B′D² ，并求出使P′D²+B′D²取得最小值时点P′的坐标；
③如图4，若点P为四边形ABCD关于A、B的等角点，且点P坐标为（1，t），求t的值；
④以四边形ABCD的一边为边画四边形，所画的四边形与四边形ABCD有公共部分，若在所画的四边形内存在一点P，使点P分别是各相邻两顶点的等角点，且四对等角都相等，请直接写出所有满足条件的点P的坐标．

查看解析收藏纠错

+选题

人数	3	4	2	1
分数	80	85	90	95

浙江省宁波市鄞州实验中学2018届九年级下学期数学3月联考试卷

一、选择题：

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨