修改时间:2024-07-12 浏览次数:1343 类型:期末考试

为了丰富社会实践活动,引导学生科学探究,学校组织七年级同学走进中国科技馆,亲近科学,感受科技魅力.来到科技馆大厅,同学们就被大厅里会“跳舞”的“小球矩阵”吸引住了(如图1).白色小球全部由计算机精准控制,每一只小球可以“悬浮”在大厅上空的不同位置,演绎着曲线、曲面、平面、文字和三维图案等各种动态造型.
已知每个小球分别由独立的电机控制.图2,图3分别是9个小球可构成的两个造型,在每个造型中,相邻小球的高度差均为a.为了使小球从造型一(如图2)变到造型二(如图3),控制电机使造型一中的②,③,④,⑥,⑦,⑧号小球同时运动,②,③,④号小球向下运动,运动速度均为3米/秒;⑥,⑦,⑧号小球向上运动,运动速度均为2米/秒,当每个小球到达造型二的相应位置时就停止运动.已知⑦号小球比②号小球晚 秒到达相应位置,问②号小球运动了多少米?
如图1,点O是弹力墙MN上一点,魔法棒从OM的位置开始绕点O向ON的位置顺时针旋转,当转到ON位置时,则从ON位置弹回,继续向OM位置旋转;当转到OM位置时,再从OM的位置弹回,继续转向ON位置,…,如此反复.按照这种方式将魔法棒进行如下步骤的旋转:第1步,从OA0(OA0在OM上)开始旋转α至OA1;第2步,从OA1开始继续旋转2α至OA2;第3步,从OA2开始继续旋转3α至OA3 , ∁….
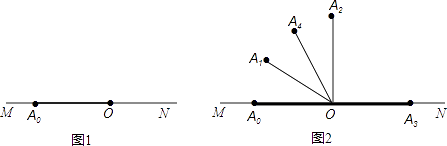
例如:当α=30°时,OA1 , OA2 , OA3 , OA4的位置如图2所示,其中OA3恰好落在ON上,∠A3OA4=120°;
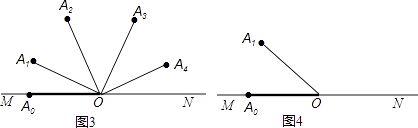
当α=20°时,OA1 , OA2 , OA3 , OA4 , OA3的位置如图3所示,
其中第4步旋转到ON后弹回,即∠A3ON+∠NOA4=80°,而OA3恰好与OA2重合.
解决如下问题:
若α<30°,且OA4所在的射线平分∠A2OA3 , 在如图5中画出OA1 , OA2 , OA3 , OA4并求出α的值;
![]()
试题篮