山东省济南市2023年中考数学真题

修改时间：2023-11-06 浏览次数：274 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 下列几何体中，主视图是三角形的为（　　　）

A . B . C . D .

查看解析收藏纠错

+选题
2. 2022年我国粮食总产量再创新高，达686530000吨．将数字686530000用科学记数法表示为（　　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图，一块直角三角板的直角顶点放在直尺的一边上．如果 $\text{[math]}$ ，那么 $\text{[math]}$ 的度数是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 实数 $\text{[math]}$ ， $\text{[math]}$ 在数轴上对应点的位置如图所示，则下列结论正确的是（　　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 下图是度量衡工具汉尺、秦权、新莽铜卡尺和商鞅方升的示意图，其中既是轴对称图形又是中心对称图形的是（　　　）

A . B . C . D .

查看解析收藏纠错

+选题
6. 下列运算正确的是（　　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都在反比例函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系为（　　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 从甲、乙、丙、丁4名同学中随机抽取2名同学参加图书节志愿服务活动，其中甲同学是女生，乙、丙、丁同学都是男生，被抽到的2名同学都是男生的概率为（　　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 为半径作弧交 $\text{[math]}$ 于点 $\text{[math]}$ ，再分别以 $\text{[math]}$ ， $\text{[math]}$ 为圆心，以大于 $\text{[math]}$ 的长为半径作弧，两弧相交于点 $\text{[math]}$ ，作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．以下结论不正确的是（　　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 定义：在平面直角坐标系中，对于点 $\text{[math]}$ ，当点 $\text{[math]}$ 满足 $\text{[math]}$ 时，称点 $\text{[math]}$ 是点 $\text{[math]}$ 的“倍增点”，已知点 $\text{[math]}$ ，有下列结论：
①点 $\text{[math]}$ ， $\text{[math]}$ 都是点 $\text{[math]}$ 的“倍增点”；
②若直线 $\text{[math]}$ 上的点A是点 $\text{[math]}$ 的“倍增点”，则点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ；
③抛物线 $\text{[math]}$ 上存在两个点是点 $\text{[math]}$ 的“倍增点”；
④若点 $\text{[math]}$ 是点 $\text{[math]}$ 的“倍增点”，则 $\text{[math]}$ 的最小值是 $\text{[math]}$ ．
其中，正确结论的个数是（　　　）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题

二、填空题

11. 因式分解: $\text{[math]}$ .

查看解析收藏纠错

+选题
12. 围棋起源于中国，棋子分黑白两色．一个不透明的盒子中装有3个黑色棋子和若干个白色棋子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑色棋子的概率是 $\text{[math]}$ ，则盒子中棋子的总个数是．

查看解析收藏纠错

+选题
13. 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有实数根，则 $\text{[math]}$ 的值可以是（写出一个即可）．

查看解析收藏纠错

+选题
14. 如图，正五边形 $\text{[math]}$ 的边长为 $\text{[math]}$ ，以 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 为半径作弧 $\text{[math]}$ ，则阴影部分的面积为（结果保留 $\text{[math]}$ ）．

查看解析收藏纠错

+选题
15. 学校提倡“低碳环保，绿色出行”，小明和小亮分别选择步行和骑自行车上学，两人各自从家同时同向出发，沿同一条路匀速前进．如图所示， $\text{[math]}$ 和 $\text{[math]}$ 分别表示两人到小亮家的距离 $\text{[math]}$ 和时间 $\text{[math]}$ 的关系，则出发h后两人相遇．

查看解析收藏纠错

+选题
16. 如图，将菱形纸片 $\text{[math]}$ 沿过点 $\text{[math]}$ 的直线折叠，使点 $\text{[math]}$ 落在射线 $\text{[math]}$ 上的点 $\text{[math]}$ 处，折痕 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长等于．

查看解析收藏纠错

+选题

三、解答题

17. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
18. 解不等式组： $\text{[math]}$ ，并写出它的所有整数解．

查看解析收藏纠错

+选题
19. 已知：如图，点 $\text{[math]}$ 为 $\text{[math]}$ 对角线 $\text{[math]}$ 的中点，过点 $\text{[math]}$ 的直线与 $\text{[math]}$ ， $\text{[math]}$ 分别相交于点 $\text{[math]}$ ， $\text{[math]}$ ．
求证： $\text{[math]}$ ．

查看解析收藏纠错

+选题
20. 图1是某越野车的侧面示意图，折线段 $\text{[math]}$ 表示车后盖，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，该车的高度 $\text{[math]}$ ．如图2，打开后备箱，车后盖 $\text{[math]}$ 落在 $\text{[math]}$ 处， $\text{[math]}$ 与水平面的夹角 $\text{[math]}$ ．

（1）求打开后备箱后，车后盖最高点 $\text{[math]}$ 到地面 $\text{[math]}$ 的距离；

（2）若小琳爸爸的身高为 $\text{[math]}$ ，他从打开的车后盖 $\text{[math]}$ 处经过，有没有碰头的危险?请说明理由．
（结果精确到 $\text{[math]}$ ，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
21. 2023年，国内文化和旅游行业复苏势头强劲．某社团对30个地区“五一”假期的出游人数进行了调查，获得了它们“五一”假期出游人数（出游人数用 $\text{[math]}$ 表示，单位：百万）的数据，并对数据进行统计整理．数据分成5组：
A组： $\text{[math]}$ ；B组： $\text{[math]}$ ；C组： $\text{[math]}$ ；D组： $\text{[math]}$ ；E组： $\text{[math]}$ ．
下面给出了部分信息：
a ． B组的数据：12，13，15，16，17，17，18，20．
b ．不完整的“五一”假期出游人数的频数分布直方图和扇形统计图如下：

请根据以上信息完成下列问题：

（1）统计图中E组对应扇形的圆心角为度；

（2）请补全频数分布直方图；

（3）这30个地区“五一”假期出游人数的中位数是百万；

（4）各组“五一”假期的平均出游人数如下表：
组别
A $\text{[math]}$
B $\text{[math]}$
C $\text{[math]}$
D $\text{[math]}$
E $\text{[math]}$
平均出游人数（百万）
5.5
16
32.5
42
50
求这30个地区“五一”假期的平均出游人数．

查看解析收藏纠错

+选题
22. 如图， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的直径， $\text{[math]}$ 为 $\text{[math]}$ 上一点，过点 $\text{[math]}$ 的切线与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，弦 $\text{[math]}$ ， $\text{[math]}$ 相交于点F．

（1）求 $\text{[math]}$ 的度数；

（2）若 $\text{[math]}$ ，求 $\text{[math]}$ 直径的长．

查看解析收藏纠错

+选题
23. 某校开设智能机器人编程的校本课程，购买了A ， B两种型号的机器人模型．A型机器人模型单价比B型机器人模型单价多200元，用2000元购买A型机器人模型和用1200元购买B型机器人模型的数量相同．

（1）求A型，B型机器人模型的单价分别是多少元?

（2）学校准备再次购买A型和B型机器人模型共40台，购买B型机器人模型不超过A型机器人模型的3倍，且商家给出了两种型号机器人模型均打八折的优惠．问购买A型和B型机器人模型各多少台时花费最少?最少花费是多少元?

查看解析收藏纠错

+选题
24. 综合与实践
如图1，某兴趣小组计划开垦一个面积为 $\text{[math]}$ 的矩形地块 $\text{[math]}$ 种植农作物，地块一边靠墙，另外三边用木栏围住，木栏总长为 $\text{[math]}$ ．

【问题提出】
小组同学提出这样一个问题：若 $\text{[math]}$ ，能否围出矩形地块？

（1）【问题探究】
小颖尝试从“函数图象”的角度解决这个问题：
设 $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ ．由矩形地块面积为 $\text{[math]}$ ，得到 $\text{[math]}$ ，满足条件的 $\text{[math]}$ 可看成是反比例函数 $\text{[math]}$ 的图象在第一象限内点的坐标；木栏总长为 $\text{[math]}$ ，得到 $\text{[math]}$ ，满足条件的 $\text{[math]}$ 可看成一次函数 $\text{[math]}$ 的图象在第一象限内点的坐标，同时满足这两个条件的 $\text{[math]}$ 就可以看成两个函数图象交点的坐标．
如图2，反比例函数 $\text{[math]}$ 的图象与直线 $\text{[math]}$ ： $\text{[math]}$ 的交点坐标为 $\text{[math]}$ 和，因此，木栏总长为 $\text{[math]}$ 时，能围出矩形地块，分别为： $\text{[math]}$ ， $\text{[math]}$ ；或 $\text{[math]}$ m ， $\text{[math]}$ m ．

根据小颖的分析思路，完成上面的填空．

（2）【类比探究】
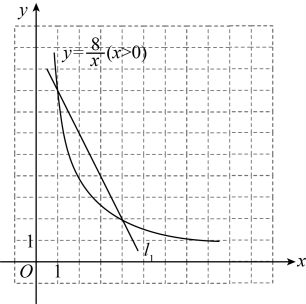
若 $\text{[math]}$ ，能否围出矩形地块？请仿照小颖的方法，在图2中画出一次函数图象并说明理由．

（3）【问题延伸】
当木栏总长为 $\text{[math]}$ 时，小颖建立了一次函数 $\text{[math]}$ ．发现直线 $\text{[math]}$ 可以看成是直线 $\text{[math]}$ 通过平移得到的，在平移过程中，当过点 $\text{[math]}$ 时，直线 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象有唯一交点．
请在图2中画出直线 $\text{[math]}$ 过点 $\text{[math]}$ 时的图象，并求出 $\text{[math]}$ 的值．

（4）【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“ $\text{[math]}$ 与 $\text{[math]}$ 图象在第一象限内交点的存在问题”．
若要围出满足条件的矩形地块，且 $\text{[math]}$ 和 $\text{[math]}$ 的长均不小于 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题
25. 在平面直角坐标系 $\text{[math]}$ 中，正方形 $\text{[math]}$ 的顶点 $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 轴上， $\text{[math]}$ ， $\text{[math]}$ ．抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ 和点 $\text{[math]}$ ．

（1）如图1，若抛物线过点 $\text{[math]}$ ，求抛物线的表达式和点 $\text{[math]}$ 的坐标；

（2）如图2，在（1）的条件下，连接 $\text{[math]}$ ，作直线 $\text{[math]}$ ，平移线段 $\text{[math]}$ ，使点 $\text{[math]}$ 的对应点 $\text{[math]}$ 落在直线 $\text{[math]}$ 上，点 $\text{[math]}$ 的对应点 $\text{[math]}$ 落在抛物线上，求点 $\text{[math]}$ 的坐标；

（3）若抛物线 $\text{[math]}$ 与正方形 $\text{[math]}$ 恰有两个交点，求 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题
26. 在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，将射线 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转90°，交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ，以线段 $\text{[math]}$ ， $\text{[math]}$ 为邻边作矩形 $\text{[math]}$ ．

（1）如图1，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的度数和 $\text{[math]}$ 的值；

（2）如图2，当点 $\text{[math]}$ 在射线 $\text{[math]}$ 上时，求线段 $\text{[math]}$ 的长；

（3）如图3，当 $\text{[math]}$ 时，在平面内有一动点 $\text{[math]}$ ，满足 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的最小值．

查看解析收藏纠错

+选题

组别	A $\text{[math]}$	B $\text{[math]}$	C $\text{[math]}$	D $\text{[math]}$	E $\text{[math]}$
平均出游人数（百万）	5.5	16	32.5	42	50

山东省济南市2023年中考数学真题

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨