修改时间:2024-07-13 浏览次数:288 类型:中考真卷

根据图中信息,解答下列问题:
②补全条形统计图(要求在条形图上方注明人数);
③扇形统计图中圆心角 ▲ 度;
|
变量a(cm) |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
|
变量h(cm) |
0 |
0.5 |
1 |
1.5 |
2 |
1.5 |
1 |
0.5 |
0 |
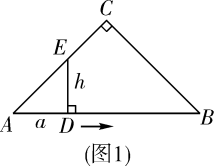
在平面直角坐标系中,以变量a的值为横坐标,变量h的值为纵坐标,描点如图2-1;以变量h的值为横坐标,变量a的值为纵坐标,描点如图2-2.
根据探究的结果,解答下列问题:
①当 时,
▲ ;当
时,
▲ .
②将图2-1,图2-2中描出的点顺次连接起来.
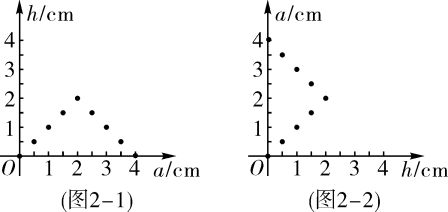
③下列说法正确的是 ▲ .(填“A”或“B”)
A.变量h是以a为自变量的函数 B.变量a是以h为自变量的函数
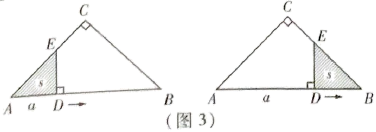
①分别求出当 和
时,s关于a的函数表达式;
②当 时,求a的值.
试题篮