备考2022年中考数学一轮复习专题：概率

修改时间：2022-01-15 浏览次数：56 类型：一轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 盒子中装有1个红球和2个绿球，每个球除颜色外都相同，从盒子中任意摸出1个球，不放回，再任意摸出1个球，两球都是绿球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 任意一个事件发生的概率p的取值范围是（）

A . 0＜P＜1 B . 0≤P＜1 C . 0＜P≤1 D . 0≤p≤1

查看解析收藏纠错

+选题
3. 小梅随机选择在下周一至周五的某一天去打新冠疫苗，则她选择在周二去打疫苗的概率为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 现有4张卡片，正面图案如图所示，它们除此之外完全相同．把这4张卡片背面朝上洗匀，从中随机抽取两张，则这两张卡片正面图案恰好是“天问”和“九章”的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

5. “十一”长假期间，某玩具超市设立了一个如图所示的可以自由转动的转盘，开展有奖购买活动，顾客购买玩具就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应奖品．下表是该活动的一组统计数据：

转动转盘的次数n	100	150	200	500	800	1000
落在“铅笔”区域的次数m	68	108	140	355	560	690
落在“铅笔”区域的频率 $\text{[math]}$	0.68	0.72	0.70	0.71	0.70	0.69

下列说法错误的是（）

A . 转动转盘20次，一定有6次获得“文具盒”铅笔文具盒 B . 转动转盘一次，获得“铅笔”的概率大约是0.70 C . 再转动转盘100次，指针落在“铅笔”区域的次数不一定是68次 D . 如果转动转盘3000次，指针落在“文具盒”区域的次数大约有900次

查看解析收藏纠错

+选题

6. 下列事件中，属于必然事件的是（）

A . 购买一张彩票，中奖 B . 射击运动员射击一次，命中10环 C . 任意画一个三角形，内角和为 $\text{[math]}$ D . 在一个只装有白球的袋中摸出红球

查看解析收藏纠错

+选题
7. 如图，直线 $\text{[math]}$ ，直线c与直线a、b都相交，从 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 这四个角中任意选取2个角，则所选取的2个角互为补角的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图①所示，一张纸片上有一个不规则的图案（图中画图部分），小雅想了解该图案的面积是多少，她采取了以下的办法：用一个长为5m，宽为3m的长方形，将不规则图案围起来，然后在适当位置随机地向长方形区域扔小球，并记录小球在不规则图案上的次数（球扔在界线上或长方形区域外不计入试验结果），她将若干次有效试验的结果绘制成了图②所示的折线统计图，由此她估计此不规则图案的面积大约为（）

A . 6m² B . 5m² C . 4m² D . 3m²

查看解析收藏纠错

+选题
9. 有一个只放满形状大小都一样的白色小球的不透明盒子，小刚想知道盒内有多少白球，于是小刚向这个盒中放了5个黑球（黑球的形状大小与白球一样），摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中80次摸到黑球，则盒中白色小球的个数可能是（）

A . 16个 B . 20个 C . 24个 D . 25个

查看解析收藏纠错

+选题
10. 一个质地均匀的小正方体，六个面分别标有数字“1”，“2”，“3”“4”，“5”，“6”，抛出小正方体后，观察朝上一面的数字，出现偶数的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

11. 如图，在实验桌上有完全相同的烧杯内装有体积相同且无色透明的3种液体，其中1杯酒精，3杯生理盐水，2杯白糖水，从中任取一杯为白糖水的概率是．

查看解析收藏纠错

+选题
12. 在学校举办的“美德少年”评选活动中，九年级一班有甲，乙，丙，丁共4名学生获奖．班主任决定在这4名获奖学生中随机选出2名学生在班级进行主题演讲，则甲被选中的概率为．

查看解析收藏纠错

+选题
13. 数据分析技术为打赢疫情防控阻击战发挥了重要作用，如图是小明同学的健康码（绿码）示意图，用黑白打印机打印于边长为 $\text{[math]}$ 的正方形区域内．为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，估计黑色部分的总面积约为 $\text{[math]}$ ．

查看解析收藏纠错

+选题
14. 如图，是两个可以自由转动的转盘，转盘各被等分为三个扇形，并分别标有2、3、4和6、7、8这6个数字，如果同时转动这两个转盘各一次（指针落在等分线上重转），转盘停止后，则指针指向的数字之和为奇数的概率为．

查看解析收藏纠错

+选题
15. 有四张大小、形状及背面完全相同的卡片，卡片正面分别画有等边三角形、正方形、平行四边形、菱形，从这四张卡片中任意抽取一张，卡片正面的图形既是轴对称图形又是中心对称图形的概率是．

查看解析收藏纠错

+选题
16. 如图所示，转盘被分成面积相等的8份，小强随机转动转盘一次，则指针指到偶数的概率是．

查看解析收藏纠错

+选题

三、综合题

17. 为倡导“低碳出行”，每年9月22日为世界无车日，2020年9月22日，由中国城市公共交通协会联合清华大学中国城市研究院共同举办的第十四届“922绿色出行日”主题活动拉开序幕，环保部门对某城市居民出行使用交通方式的情况进行了问卷调查，将收回的问卷调查结果整理后，绘制了如下不完整的统计图，其中“骑自行车、电动车”所在的扇形的圆心角是162°．

请根据以上信息解答下列问题：

（1）请补全条形统计图．

（2）如果绿色出行是指“骑自行车、电动车”和“坐公交车”，计算绿色出行在所有交通方式中的频率，并在50万人口的城市中选择绿色出行的共有多少人．

（3）若参与问卷调查的人中选择“其他”交通方式的有两名女性，其余为男性，现从中随机选取两人进行跟踪调查，请借助树状图或者表格，求出恰好选到1男1女的概率．

查看解析收藏纠错

+选题
18. 2019年12月以来，湖北省武汉市部分医院陆续发现不明原因肺炎病例，现已证实该肺炎为一种新型冠状病毒感染的肺炎，其传染性较强.为了有效地避免交叉感染，需要采取以下防护措施：①戴口罩；②勤洗手；③少出门；④重隔离；⑤捂口鼻；⑥谨慎吃．某公司为了解员工对防护措施的了解程度（包括不了解、了解很少、基本了解和很了解），通过网上问卷调查的方式进行了随机抽样调查（每名员工必须且只能选择一项），并将调查结果绘制成如下两幅统计图．

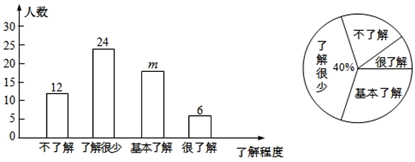
请你根据上面的信息，解答下列问题

（1）本次共调查了名员工，条形统计图中 $\text{[math]}$ ；

（2）若该公司共有员工1000名，请你估计不了解防护措施的人数；

（3）在调查中，发现有4名员工对防护措施很了解，其中有3名男员工、1名女员工.若准备从他们中随机抽取2名，让其在公司群内普及防护措施，求恰好抽中一男一女的概率．

查看解析收藏纠错

+选题
19. 学完统计知识后，小明对同学们最近一周的睡眠情况进行随机抽样调查，得到他们每日平均睡眠时长 $\text{[math]}$ （单位：小时）的一组数据，将所得数据分为四组（A： $\text{[math]}$ ；B： $\text{[math]}$ ；C： $\text{[math]}$ ；D： $\text{[math]}$ ），并绘制成如下两幅不完整的统计图．

根据以上信息，解答下列问题：

（1）小明一共抽样调查了名同学；在扇形统计图中，表示D组的扇形圆心角的度数为；

（2）将条形统计图补充完整；

（3）小明所在学校共有I400名学生，估计该校最近一周大约有多少名学生睡眠时长不足8小时?

（4） A组的四名学生是2名男生和2名女生，若从他们中任选2人了解最近一周睡眠时长不足8小时的原因，试求恰好选中1名男生和I名女生的概率．

查看解析收藏纠错

+选题
20. 如图，有两部不同型号的手机(分别记为A，B)和与之匹配的2个保护盖(分别记为a，b)散乱地放在桌子上．

（1）若从手机中随机取一部，再从保护盖中随机取一个，求恰好匹配的概率；

（2）若从手机和保护盖中随机取两个，用画树状图法或列表法求恰好匹配的概率．

查看解析收藏纠错

+选题
21. 随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样、便捷．某校数学兴趣小组设计了一份调查问卷，要求每人选且只选一种你最喜欢的支付方式．现将调查结果进行统计并绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：

（1）这次活动共调查了人；在扇形统计图中，表示“支付宝”支付的扇形圆心角的度数为；

（2）将条形统计图补充完整．观察此图，支付方式的“众数”是“”；

（3）在一次购物中，小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付，请用画树状图或列表格的方法，求出两人恰好选择同一种支付方式的概率．

查看解析收藏纠错

+选题
22. 在一个不透明的盒子中，共有“一白三黑”4颗围棋子，它们除了颜色之外没有其他区别．

（1）随机地从盒中提出1颗棋子，则提出黑子的概率是多少

（2）随机地从盒中同时提出2颗棋子，请你用画树状图或列表的方法表示所有等可能的结果，并求恰好提出“一黑一白"2颗棋子的概率．

查看解析收藏纠错

+选题

23. 在一只不透明的口袋里，装有若干个除了颜色外均相同的小球，某数学学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．如表是活动进行中的一组统计数据：

摸球的次数 $\text{[math]}$	100	150	200	500	800	1000
摸到白球的次数 $\text{[math]}$	59	96	$\text{[math]}$	295	480	601
摸到白球的频率 $\text{[math]}$	$\text{[math]}$	0.64	0.58	0.59	0.60	0.601

（1）请直接写出上表中的 $\text{[math]}$ ， $\text{[math]}$ ；

（2）请直接写出事件“摸到白球”的概率的估计值是（精确到 $\text{[math]}$ ）；

（3）如果袋中有12个白球，请你估计袋中除了白球外，还有多少个其它颜色的球？

查看解析收藏纠错

+选题

24. 为了保护学生视力，防止学生沉迷网络和游戏，促进学生身心健康发展，教育办公厅于2021年1月15日颁发了《教育部办公厅关于加强中小学生手机管理工作的通知》为贯彻《通知》精神，学校组织该主题漫画比赛．现在小雪和小英想通过设计一个游戏来决定谁去参赛．游戏规则如下：有一个可自由转动的转盘，被分成了三个大小相同的扇形，分别标有数字2，3，4；另有一个不透明的瓶子，装有分别标有数字1，3，5的三个完全相同的小球．先转动一次转盘，停止后记下指针指向的数字（若指针指在分界线上则重转），再从瓶子中随机取出一个小球，记下小球上的数字．若得到的两数字之和大于6，则小雪参赛；若得到的两数字之和小于6，则小英参赛．

（1）请用列表或画树状图的方法表示出所有可能出现的结果；

（2）此游戏公平吗？请说明理由．

查看解析收藏纠错

+选题
25. 在甲、乙两个不透明的口袋中，分别有大小、材质完全相同的小球，其中甲口袋中的小球上分别标有数字 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，乙口袋中的小球上分别标有数字 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，先从甲口袋中任意摸出一个小球，记下数字为 $\text{[math]}$ ，再从乙口袋中任意摸出一个小球，记下数字为 $\text{[math]}$ ．

（1）请用列表或画树状图的方法表示出所有 $\text{[math]}$ 可能的结果．

（2）若 $\text{[math]}$ ， $\text{[math]}$ 都是方程 $\text{[math]}$ 的解时，则小明获胜；若 $\text{[math]}$ ， $\text{[math]}$ 都不是方程 $\text{[math]}$ 的解时，则小利获胜，问他们两人谁获胜的概率大？并说明理由．

查看解析收藏纠错

+选题
26. 电影“长津湖”的热映，让今年国庆节多了几分英雄气．现有电影票一张，明明和磊磊打算通过玩掷骰子的游戏决定谁拥有．游戏规则是：在一枚均匀的正方体骰子的每个面上分别标上数字1、2、3、4、5、6．明明和磊磊各掷一次骰子，若两次朝上的点数之和是3的倍数，则明明获胜，电影票归明明所有，否则磊磊获胜．

（1）用画树状图或列表的方法表示所有可能的结果；

（2）你认为这个游戏规则对明明和磊磊公平吗？请说明理由．

查看解析收藏纠错

+选题

27. 王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球试验，每次摸出一个球（有放回），表格是活动进行中的一组统计数据：

摸球的次数 $\text{[math]}$	100	150	200	500	800	1000
摸到黑球的次数 $\text{[math]}$	23	31	60	130	203	251
摸到黑球的频率 $\text{[math]}$	0.23	0.21	0.30	0.26	0.235	0.251

（1）根据上表数据估计从袋中摸出一个球是黑球的概率是；（精确到 $\text{[math]}$ ）

（2）估算袋中白球的个数.

查看解析收藏纠错

+选题

备考2022年中考数学一轮复习专题：概率

一、单选题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨