广西百色市2021年中考数学试卷

修改时间：2024-07-13 浏览次数：335 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. ﹣2022的相反数是（）

A . ﹣2022 B . 2022 C . ±2022 D . 2021

查看解析收藏纠错

+选题
2. 如图，与∠1是内错角的是（）

A . ∠2 B . ∠3 C . ∠4 D . ∠5

查看解析收藏纠错

+选题
3. 骰子各面上的点数分别是1，2，…，6，抛掷一枚骰子，点数是偶数的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

查看解析收藏纠错

+选题
4. 已知∠α＝25°30′，则它的余角为（）

A . 25°30′ B . 64°30′ C . 74°30′ D . 154°30′

查看解析收藏纠错

+选题
5. 方程 $\text{[math]}$ ＝ $\text{[math]}$ 的解是（）.

A . x＝﹣2 B . x＝﹣1 C . x＝1 D . x＝3

查看解析收藏纠错

+选题
6. 一组数据4，6，x，7，10的众数是7，则这组数据的平均数是（）

A . 5 B . 6.4 C . 6.8 D . 7

查看解析收藏纠错

+选题
7. 下列各式计算正确的是（）

A . 3³＝9 B . （a﹣b）²＝a²﹣b² C . 2 $\text{[math]}$ ＋3 $\text{[math]}$ ＝5 $\text{[math]}$ D . （2a²b）³＝8a⁸b³

查看解析收藏纠错

+选题
8. 下列展开图中，不是正方体展开图的是（）

A . B . C . D .

查看解析收藏纠错

+选题
9. 如图，在⊙O中，尺规作图的部分作法如下：（1）分别以弦AB的端点A、B为圆心，适当等长为半径画弧，使两弧相交于点M；（2）作直线OM交AB于点N.若OB＝10，AB＝16，则tan∠B等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 当x＝﹣2时，分式 $\text{[math]}$ 的值是（）

A . ﹣15 B . ﹣3 C . 3 D . 15

查看解析收藏纠错

+选题
11. 下列四个命题：①直径是圆的对称轴；②若两个相似四边形的相似比是1：3，则它们的周长比是1：3，面积比是1：6；③同一平面内垂直于同一直线的两条直线互相平行；④对角线相等且互相垂直的平行四边形是正方形.其中真命题有（）

A . ①③ B . ①④ C . ③④ D . ②③④

查看解析收藏纠错

+选题
12. 如图，矩形ABCD各边中点分别是E、F、G、H，AB＝2 $\text{[math]}$ ，BC＝2，M为AB上一动点，过点M作直线l⊥AB，若点M从点A开始沿着AB方向移动到点B即停（直线l随点M移动），直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM＝x，则S关于x的函数图象大致是（）

A . B . C . D .

查看解析收藏纠错

+选题

二、填空题

13. $\text{[math]}$ 的倒数是.

查看解析收藏纠错

+选题
14. 某公司开展“爱心公益”活动，将价值16000元的物品捐赠给山区小学，数据16000用科学记数法表示为.

查看解析收藏纠错

+选题
15. 如图，是一组数据的折线统计图，则这组数据的中位数是.

查看解析收藏纠错

+选题
16. 实数 $\text{[math]}$ 的整数部分是.

查看解析收藏纠错

+选题
17. 数学活动小组为测量山顶电视塔的高度，在塔的椭圆平台遥控无人机.当无人机飞到点P处时，与平台中心O点的水平距离为15米，测得塔顶A点的仰角为30°，塔底B点的俯角为60°，则电视塔的高度为米.

查看解析收藏纠错

+选题
18. 如图，△ABC中，AB＝AC，∠B＝72°，∠ACB的平分线CD交AB于点D，则点D是线段AB的黄金分割点.若AC＝2，则BD＝.

查看解析收藏纠错

+选题

三、解答题

19. 计算：（π﹣1）⁰＋| $\text{[math]}$ ﹣2|﹣（ $\text{[math]}$ ）^﹣¹＋tan60°.

查看解析收藏纠错

+选题
20. 解不等式组 $\text{[math]}$ ，并把解集在数轴上表示出来.

查看解析收藏纠错

+选题
21. 如图，O为坐标原点，直线l⊥y轴，垂足为M，反比例函数y＝ $\text{[math]}$ （k≠0）的图象与l交于点A（m，3），△AOM的面积为6

（1）求m、k的值；

（2）在x轴正半轴上取一点B，使OB＝OA，求直线AB的函数表达式.

查看解析收藏纠错

+选题
22. 如图，点D、E分别是AB、AC的中点，BE、CD相交于点O，∠B＝∠C，BD＝CE.求证：

（1） OD＝OE；

（2） △ABE≌△ACD.

查看解析收藏纠错

+选题
23. 为了解某校九年级500名学生周六做家务的情况，黄老师从中随机抽取了部分学生进行调查，将他们某一周六做家务的时间t（小时）分成四类（A：0≤t＜1，B：1≤t＜2，C：2≤t＜3，D：t≥3），并绘制如下不完整的统计表和扇形统计图.

类别

A

B

C

D

人数

2

18

3

根据所给信息：

（1）求被抽查的学生人数；

（2）周六做家务2小时以上（含2小时）为“热爱劳动”，请你估计该校九年级“热爱劳动”的学生人数；

（3）为让更多学生积极做家务，从A类与D类学生中任选2人进行交流，求恰好选中A类与D类各一人的概率（用画树状图或列表法把所有可能结果表示出来）.

查看解析收藏纠错

+选题
24. 据国际田联《田径场地设施标准手册》，400米标准跑道由两个平行的直道和两个半径相等的弯道组成，有8条跑道，每条跑道宽1.2米，直道长87米；跑道的弯道是半圆形，环形跑道第一圈（最内圈）弯道半径为35.00米到38.00米之间.
某校据国际田联标准和学校场地实际，建成第一圈弯道半径为36米的标准跑道.小王同学计算了各圈的长：

第一圈长：87×2＋2π（36＋1.2×0）≈400（米）；

第二圈长：87×2＋2π（36＋1.2×1）≈408（米）；

第三圈长：87×2＋2π（36＋1.2×2）≈415（米）；

……

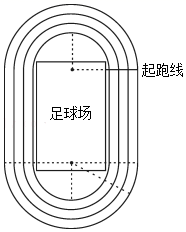
请问：

（1）第三圈半圆形弯道长比第一圈半圆形弯道长多多少米？小王计算的第八圈长是多少？

（2）小王紧靠第一圈边线逆时针跑步、邓教练紧靠第三圈边线顺时针骑自行车（均以所靠边线长计路程），在如图的起跑线同时出发，经过20秒两人在直道第一次相遇.若邓教练平均速度是小王平均速度的2倍，求他们的平均速度各是多少？
（注：在同侧直道，过两人所在点的直线与跑道边线垂直时，称两人直道相遇）

查看解析收藏纠错

+选题
25. 如图，PM、PN是⊙O的切线，切点分别是A、B，过点O的直线CE∥PN，交⊙O于点C、D，交PM于点E，AD的延长线交PN于点F，若BC∥PM.

（1）求证：∠P＝45°；

（2）若CD＝6，求PF的长.

查看解析收藏纠错

+选题
26. 已知O为坐标原点，直线l：y＝﹣ $\text{[math]}$ x＋2与x轴、y轴分别交于A、C两点，点B（4，2）关于直线l的对称点是点E，连接EC交x轴于点D.

（1）求证：AD＝CD；

（2）求经过B、C、D三点的抛物线的函数表达式；

（3）当x＞0时，抛物线上是否存在点P，使S_△PBC＝ $\text{[math]}$ S_△OAE？若存在，求点P的坐标；若不存在，说明理由.

查看解析收藏纠错

+选题

类别	A	B	C	D
人数	2	18		3

广西百色市2021年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨