河南省2021年中考数学试卷

1. 实数-2的绝对值是（）

A . -2 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 河南人民济困最“给力！”，据报道，2020年河南人民在济困方面捐款达到 $\text{[math]}$ 亿元数据“ $\text{[math]}$ 亿”用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图是由8个相同的小正方体组成的几何体，其主视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 关于菱形的性质，以下说法不正确的是（）

A . 四条边相等 B . 对角线相等 C . 对角线互相垂直 D . 是轴对称图形

查看解析收藏纠错

+选题
7. 若方程 $\text{[math]}$ 没有实数根，则 $\text{[math]}$ 的值可以是（）

A . -1 B . $\text{[math]}$ C . 1 D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 现有4张卡片，正面图案如图所示，它们除此之外完全相同.把这4张卡片背面朝上洗匀，从中随机抽取两张，则这两张卡片正面图案恰好是“天问”和“九章”的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图， $\text{[math]}$ 的顶点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 轴的正半轴上，延长 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ .将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转得到 $\text{[math]}$ ，当点 $\text{[math]}$ 的对应点 $\text{[math]}$ 落在 $\text{[math]}$ 上时， $\text{[math]}$ 的延长线恰好经过点 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图1，矩形 $\text{[math]}$ 中，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，点 $\text{[math]}$ 沿 $\text{[math]}$ 从点 $\text{[math]}$ 运动到点 $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ 两点间的距离为 $\text{[math]}$ ， $\text{[math]}$ ，图2是点 $\text{[math]}$ 运动时 $\text{[math]}$ 随 $\text{[math]}$ 变化的关系图象，则 $\text{[math]}$ 的长为（）

A . 4 B . 5 C . 6 D . 7

查看解析收藏纠错

+选题

11. 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是.

查看解析收藏纠错

+选题
12. 请写出一个图象经过原点的函数的解析式.

查看解析收藏纠错

+选题
13. 某外贸公司要出口一批规格为 $\text{[math]}$ 克/盒的红枣，现有甲、乙两个厂家提供货源，它们的价格相同，品质也相近.质检员从两厂的产品中各随机抽取 $\text{[math]}$ 盒进行检测，测得它们的平均质量均为 $\text{[math]}$ 克，每盒红枣的质量如图所示，则产品更符合规格要求的厂家是.（填“甲”或“乙”）

查看解析收藏纠错

+选题
14. 如图所示的网格中，每个小正方形的边长均为 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 均在小正方形的顶点上，且点 $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

查看解析收藏纠错

+选题
15. 小华用一张直角三角形纸片玩折纸游戏，如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .第一步，在 $\text{[math]}$ 边上找一点 $\text{[math]}$ ，将纸片沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 落在 $\text{[math]}$ 处，如图2，第二步，将纸片沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 落在 $\text{[math]}$ 处，如图3.当点 $\text{[math]}$ 恰好在原直角三角形纸片的边上时，线段 $\text{[math]}$ 的长为.

查看解析收藏纠错

+选题

16.

（1）计算： $\text{[math]}$ ；

（2）化简： $\text{[math]}$ .

查看解析收藏纠错

+选题

17. 2021年4月，教育部印发《关于进一步加强中小学生睡眠管理工作的通知》，明确要求初中生每天睡眠时间应达到9小时.某初级中学为了解学生睡眠时间的情况，从本校学生中随机抽取500名进行卷调查，并将调查结果用统计图描述如下.

调查问卷

1近两周你平均每天睡眠时间大约是小时.

如果你平均每天睡眠时间不足9小时，请回答第2个问题

2影响你睡眠时间的主要原因是 .（单选）

A.校内课业负担重 B.校外学习任务重 C.学习效率低 D.其他

平均每天睡眠时间 $\text{[math]}$ （时）分为 $\text{[math]}$ 组：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ .

根据以上信息，解答下列问题：

（1）本次调查中，平均每天睡眠时间的中位数落在第（填序号）组，达到 $\text{[math]}$ 小时的学生人数占被调查人数的百分比为；

（2）请对该校学生睡眠时间的情况作出评价，并提出两条合理化建议.

查看解析收藏纠错

+选题

18. 如图，大、小两个正方形的中心均与平面直角坐标系的原点O重合，边分别与坐标轴平行，反比例函数 $\text{[math]}$ 的图象与大正方形的一边交于点A(1，2)，且经过小正方形的顶点B.

（1）求反比例函数的解析式；

（2）求图中阴影部分的面积.

查看解析收藏纠错

+选题
19. 开凿于北魏孝文帝年间的龙门石窟是中国石刻艺术瑰宝，卢舍那佛像是石窟中最大的佛像.某数学活动小组到龙门石窟景区测量这尊佛像的高度.如图，他们选取的测量点 $\text{[math]}$ 与佛像 $\text{[math]}$ 的底部 $\text{[math]}$ 在同一水平线上.已知佛像头部 $\text{[math]}$ 为 $\text{[math]}$ ，在 $\text{[math]}$ 处测得佛像头顶部 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，头底部 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，求佛像 $\text{[math]}$ 的高度（结果精确到 $\text{[math]}$ .参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
20. 在古代，智慧的劳动人民已经会使用“石磨”，其原理为在磨盘的边缘连接一个固定长度的“连杆”，推动“连杆”带动磨盘转动，将粮食磨碎，物理学上称这种动力传输工具为“曲柄连杆机构”.小明受此启发设计了一个“双连杆机构”，设计图如图1，两个固定长度的“连杆” $\text{[math]}$ ， $\text{[math]}$ 的连接点 $\text{[math]}$ 在 $\text{[math]}$ 上，当点 $\text{[math]}$ 在 $\text{[math]}$ 上转动时，带动点 $\text{[math]}$ ， $\text{[math]}$ 分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上滑动， $\text{[math]}$ .当 $\text{[math]}$ 与 $\text{[math]}$ 相切时，点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 上，如图2.

请仅就图2的情形解答下列问题.

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ 的半径为 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题
21. 猕猴嬉戏是王屋山景区的一大特色，猕猴玩偶非常畅销.小李在某网店选中 $\text{[math]}$ ， $\text{[math]}$ 两款猕猴玩偶，决定从该网店进货并销售.两款玩偶的进货价和销售价如下表：

类别

价格

$\text{[math]}$ 款玩偶

$\text{[math]}$ 款玩偶

进货价（元/个）

40

30

销售价（元/个）

56

45

（1）第一次小李用1100元购进了 $\text{[math]}$ ， $\text{[math]}$ 两款玩偶共30个，求两款玩偶各购进多少个；

（2）第二次小李进货时，网店规定 $\text{[math]}$ 款玩偶进货数量不得超过 $\text{[math]}$ 款玩偶进货数量的一半.小李计划购进两款玩偶共30个，应如何设计进货方案才能获得最大利润，最大利润是多少？

（3）小李第二次进货时采取了（2）中设计的方案，并且两次购进的玩偶全部售出，请从利润率的角度分析，对于小李来说哪一次更合算？
（注：利润率 $\text{[math]}$ ）

查看解析收藏纠错

+选题
22. 如图，抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点A(2，0)和点 $\text{[math]}$ .

（1）求 $\text{[math]}$ 和 $\text{[math]}$ 的值；

（2）求点 $\text{[math]}$ 的坐标，并结合图象写出不等式 $\text{[math]}$ 的解集；

（3）点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的一个动点，将点 $\text{[math]}$ 向左平移 $\text{[math]}$ 个单位长度得到点 $\text{[math]}$ ，若线段 $\text{[math]}$ 与抛物线只有一个公共点，直接写出点 $\text{[math]}$ 的横坐标 $\text{[math]}$ 的取值范围.

查看解析收藏纠错

+选题

23. 下面是某数学兴趣小探究用不同方法作一角的平分线的讨论片段.请仔细阅读，并完成相应的任务.

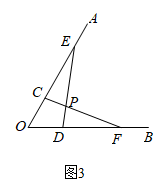
小明：如图1，（1）分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上截取 $\text{[math]}$ ， $\text{[math]}$ （点 $\text{[math]}$ ， $\text{[math]}$ 不重合）；（2）分别作线段 $\text{[math]}$ ， $\text{[math]}$ 的垂直平分线 $\text{[math]}$ ， $\text{[math]}$ ，交点为 $\text{[math]}$ ，垂足分别为点 $\text{[math]}$ ， $\text{[math]}$ ；（3）作射线 $\text{[math]}$ ，射线 $\text{[math]}$ 即为 $\text{[math]}$ 的平分线.简述理由如下：

由作图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，所以 $\text{[math]}$ ，则 $\text{[math]}$ ，即射线 $\text{[math]}$ 是 $\text{[math]}$ 的平分线.

小军：我认为小明的作图方法很有创意，但是大麻烦了，可以改进如下，如图2.（1）分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上截取 $\text{[math]}$ ， $\text{[math]}$ （点 $\text{[math]}$ ， $\text{[math]}$ 不重合）；（2）连接 $\text{[math]}$ ， $\text{[math]}$ ，交点为 $\text{[math]}$ ；（3）作射线 $\text{[math]}$ ，射线 $\text{[math]}$ 即为 $\text{[math]}$ 的平分线.

……

任务：

（1）小明得出 $\text{[math]}$ 的依据是.（填序号）

① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ .

（2）小军作图得到的射线 $\text{[math]}$ 是 $\text{[math]}$ 的平分线吗？请判断并说明理由；

（3）如图3，已知 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ .点 $\text{[math]}$ ， $\text{[math]}$ 分别为射线 $\text{[math]}$ ， $\text{[math]}$ 上的动点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，交点为 $\text{[math]}$ ，当 $\text{[math]}$ 时，直接写出线段 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题

河南省2021年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

河南省2021年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨