20. 电子体重科读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻R
1 , R
1与踏板上人的质量m之间的函数关系式为R
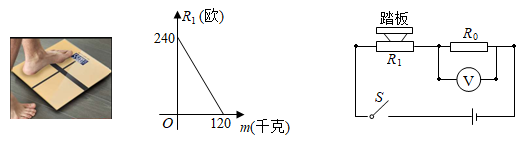
1=km+b(其中k,b为常数,0≤m≤120),其图象如图1所示;图2的电路中,电源电压恒为8伏,定值电阻R
0的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为U
0 , 该读数可以换算为人的质量m,
温馨提示:①导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I=  ;
;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压.
;
