江苏省扬州市2021年中考数学试卷

1. 实数100的倒数是（）

A . 100 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 把图中的纸片沿虚线折叠，可以围成一个几何体，这个几何体的名称是（）

A . 五棱锥 B . 五棱柱 C . 六棱锥 D . 六棱柱

查看解析收藏纠错

+选题
3. 下列生活中的事件，属于不可能事件的是（）

A . 3天内将下雨 B . 打开电视，正在播新闻 C . 买一张电影票，座位号是偶数号 D . 没有水分，种子发芽

查看解析收藏纠错

+选题
4. 不论x取何值，下列代数式的值不可能为0的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图，点A、B、C、D、E在同一平面内，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，在 $\text{[math]}$ 的正方形网格中有两个格点A、B，连接 $\text{[math]}$ ，在网格中再找一个格点C，使得 $\text{[math]}$ 是等腰直角三角形，满足条件的格点C的个数是（）

A . 2 B . 3 C . 4 D . 5

查看解析收藏纠错

+选题
7. 如图，一次函数 $\text{[math]}$ 的图像与x轴、y轴分别交于点A、B，把直线 $\text{[math]}$ 绕点B顺时针旋转 $\text{[math]}$ 交x轴于点C，则线段 $\text{[math]}$ 长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，点P是函数 $\text{[math]}$ 的图像上一点，过点P分别作x轴和y轴的垂线，垂足分别为点A、B，交函数 $\text{[math]}$ 的图像于点C、D，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，其中 $\text{[math]}$ ，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ，其中正确的是（）

A . ①② B . ①③ C . ②③ D . ①

查看解析收藏纠错

+选题

9. 2021年扬州世界园艺博览会以“绿色城市，健康生活”为主题，在某搜索引擎中输入“扬州世界园艺博览会”约有3020000个相关结果，数据3020000用科学记数法表示为.

查看解析收藏纠错

+选题
10. 计算： $\text{[math]}$ .

查看解析收藏纠错

+选题
11. 在平面直角坐标系中，若点 $\text{[math]}$ 在第二象限，则整数m的值为.

查看解析收藏纠错

+选题
12. 已知一组数据：a、4、5、6、7的平均数为5，则这组数据的中位数是.

查看解析收藏纠错

+选题
13. 扬州雕版印刷技艺历史悠久，元代数学家朱世杰的《算学启蒙》一书曾刻于扬州，该书是中国较早的数学著作之一，书中记载一道问题：“今有良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之？”题意是：快马每天走240里，慢马每天走150里，慢马先走12天，试问快马几天追上慢马？答：快马天追上慢马.

查看解析收藏纠错

+选题
14. 如图是某圆柱体果罐，它的主视图是边长为 $\text{[math]}$ 的正方形，该果罐侧面积为 $\text{[math]}$ .

查看解析收藏纠错

+选题
15. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点D是 $\text{[math]}$ 的中点，过点D作 $\text{[math]}$ ，垂足为点E，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
16. 如图，在 $\text{[math]}$ 中，点E在 $\text{[math]}$ 上，且 $\text{[math]}$ 平分 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积为.

查看解析收藏纠错

+选题
17. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，矩形 $\text{[math]}$ 的顶点D、E在 $\text{[math]}$ 上，点F、G分别在 $\text{[math]}$ 、 $\text{[math]}$ 上，若 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

查看解析收藏纠错

+选题
18. 将黑色圆点按如图所示的规律进行排列，图中黑色圆点的个数依次为：1，3，6，10，……，将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据，则新数据中的第33个数为.

查看解析收藏纠错

+选题

19. 计算或化简：

（1） $\text{[math]}$ ；

（2） $\text{[math]}$ .

查看解析收藏纠错

+选题
20. 已知方程组 $\text{[math]}$ 的解也是关于x、y的方程 $\text{[math]}$ 的一个解，求a的值.

查看解析收藏纠错

+选题
21. 为推进扬州市“青少年茁壮成长工程”，某校开展“每日健身操”活动，为了解学生对“每日健身操”活动的喜欢程度，随机抽取了部分学生进行调查，将调查信息结果绘制成如下尚不完整的统计图表：
抽样调查各类喜欢程度人数分布扇形统计图

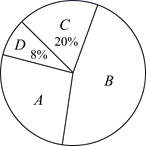
A.非常喜欢 B.比较喜欢 C.无所谓 D.不喜欢

抽样调查各类喜欢程度人数统计表

喜欢程度

人数

A.非常喜欢

50人

B.比较喜欢

m人

C.无所谓

n人

D.不喜欢

16人

根据以上信息，回答下列问题：

（1）本次调查的样本容量是；

（2）扇形统计图中表示A程度的扇形圆心角为 $\text{[math]}$ ，统计表中 $\text{[math]}$ ；

（3）根据抽样调查的结果，请你估计该校2000名学生中大约有多少名学生喜欢“每日健身操”活动（包含非常喜欢和比较喜欢）.

查看解析收藏纠错

+选题
22. 一张圆桌旁设有4个座位，丙先坐在了如图所示的座位上，甲、乙2人等可能地坐到①、②、③中的2个座位上.

（1）甲坐在①号座位的概率是；

（2）用画树状图或列表的方法，求甲与乙相邻而坐的概率.

查看解析收藏纠错

+选题
23. 为保障新冠病毒疫苗接种需求，某生物科技公司开启“加速”模式，生产效率比原先提高了20%，现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天，问原先每天生产多少万剂疫苗？

查看解析收藏纠错

+选题
24. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 的角平分线交 $\text{[math]}$ 于点D， $\text{[math]}$ .

（1）试判断四边形 $\text{[math]}$ 的形状，并说明理由；

（2）若 $\text{[math]}$ ，且 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积.

查看解析收藏纠错

+选题
25. 如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ，以点B为圆心， $\text{[math]}$ 长为半径作 $\text{[math]}$ ，交 $\text{[math]}$ 于点E.

（1）试判断 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求图中阴影部分的面积.

查看解析收藏纠错

+选题
26. 如图，在平面直角坐标系中，二次函数 $\text{[math]}$ 的图像与x轴交于点. $\text{[math]}$ 、 $\text{[math]}$ ，与y轴交于点C.

（1） $\text{[math]}$ ， $\text{[math]}$ ；

（2）若点D在该二次函数的图象上，且 $\text{[math]}$ ，求点D的坐标；

（3）若点P是该二次函数图象上位于x轴上方的一点，且 $\text{[math]}$ ，直接写出点P的坐标.

查看解析收藏纠错

+选题
27. 在一次数学探究活动中，李老师设计了一份活动单：

已知线段 $\text{[math]}$ ，使用作图工具作 $\text{[math]}$ ，尝试操作后思考：

（ 1 ）这样的点A唯一吗？

（ 2 ）点A的位置有什么特征？你有什么感悟？

“追梦”学习小组通过操作、观察、讨论后汇报：点A的位置不唯一，它在以 $\text{[math]}$ 为弦的圆弧上（点B、C除外），…….小华同学画出了符合要求的一条圆弧（如图1）.

（1）小华同学提出了下列问题，请你帮助解决.
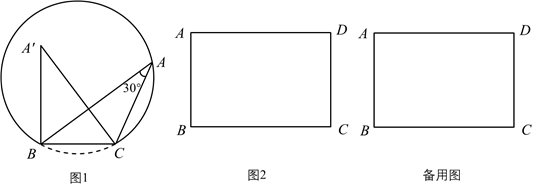
①该弧所在圆的半径长为；

② $\text{[math]}$ 面积的最大值为；

（2）经过比对发现，小明同学所画的角的顶点不在小华所画的圆弧上，而在如图1所示的弓形内部，我们记为 $\text{[math]}$ ，请你利用图1证明 $\text{[math]}$ ；

（3）请你运用所学知识，结合以上活动经验，解决问题：如图2，已知矩形 $\text{[math]}$ 的边长 $\text{[math]}$ ， $\text{[math]}$ ，点P在直线 $\text{[math]}$ 的左侧，且 $\text{[math]}$ .
①线段 $\text{[math]}$ 长的最小值为；

②若 $\text{[math]}$ ，则线段 $\text{[math]}$ 长为.

查看解析收藏纠错

+选题