修改时间:2024-07-13 浏览次数:191 类型:中考模拟
列表:下表是 与
的几组对应值,其中
▲ .
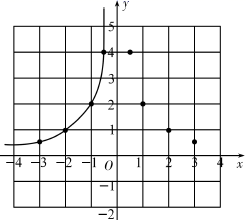
| | | -3 | -2 | -1 | | | 1 | 2 | 3 | |
| | | | 1 | 2 | 4 | 4 | 2 | | | |
描点:根据表中各组对应值 ,在平面直角坐标系中描出了各点;
连线:用平滑的曲线顺次连接各点,画出了部分图象请你把图象补充完整;
①;
②;
②探究思考:将①中“直线 ”改为“直线
”,其他条件不变,则
;
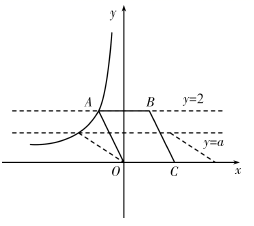
③类比猜想:若直线 交函数
的图象于
,
两点,连接
,过点
作
交
轴于
,则
.
试题篮