福建省2021年数学中考精准模拟试卷（三）

1. -2的相反数是（）

A . 2 B . -2 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 世界文化遗产—长城的总长约为 $\text{[math]}$ ，数据2100000用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 在数轴上，表示实数 $\text{[math]}$ 的点如图所示，则 $\text{[math]}$ 的值可以为（）

A . -4.5 B . -0.5 C . 0 D . 0.5

查看解析收藏纠错

+选题
4. 如图，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转，得到△ADE，点D恰好落在直线BC上，则旋转角的度数为（）

A . 70° B . 80° C . 90° D . 100°

查看解析收藏纠错

+选题
5. 某班级组织活动，为了解同学们喜爱的体育运动项目，设计了如下尚不完整的调查问卷：
调查问卷    ________年________月________日

你平时最喜欢的一种体育运动项目是（   ）（单选）

A.        B.        C.        D.其他运动项目

准备在“①室外体育运动，②篮球，③足球，④游泳，⑤球类运动”中选取三个作为该调查问卷问题的备选项目，选取合理的是（   ）

A . ①②③ B . ①③⑤ C . ②③④ D . ②④⑤

查看解析收藏纠错

+选题
6. 如图，图2是图1中长方体的三视图，若该长方体主视图的面积是 $\text{[math]}$ ，左视图的面积是 $\text{[math]}$ ，则其俯视图的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . -2 B . -1 C . 0 D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 下列性质中，等腰三角形具有而直角三角形不一定具有的是（）

A . 两边之和大于第三边 B . 有一个角的平分线垂直于这个角的对边 C . 有两个锐角的和等于90° D . 内角和等于180°

查看解析收藏纠错

+选题
9. 小明在学完《解直角三角形》一章后，利用测角仪和校园旗杆的拉绳测量校园旗杆的高度，如图，旗杆 $\text{[math]}$ 的高度与拉绳 $\text{[math]}$ 的长度相等，小明先将 $\text{[math]}$ 拉到 $\text{[math]}$ 的位置，测得 $\text{[math]}$ 为水平线），测角仪 $\text{[math]}$ 的高度为 $\text{[math]}$ 米，则旗杆 $\text{[math]}$ 的高度为（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

查看解析收藏纠错

+选题
10. 已知非负数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ 且 $\text{[math]}$ ，设 $\text{[math]}$ 的最大值为 $\text{[math]}$ ，最小值为 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . 16 B . 15 C . 9 D . 7

查看解析收藏纠错

+选题

11. 计算： $\text{[math]}$ .

查看解析收藏纠错

+选题
12. 在一个不透明的盒子里，装有10个红球和5个蓝球，每个球除颜色外都相同，从中任意摸出一个球，摸到蓝球的概率是.

查看解析收藏纠错

+选题
13. 不等式x+3＞5的解集为．

查看解析收藏纠错

+选题
14. 在半径为12的圆中， $\text{[math]}$ 圆心角所对的弧长是.

查看解析收藏纠错

+选题
15. 在平面直角坐标系中有一个轴对称图形只有一条对称轴，其中点 $\text{[math]}$ 和点 $\text{[math]}$ 是这个图形上的一对称点，若此图形上另有一点 $\text{[math]}$ ，则点 $\text{[math]}$ 的对称点的坐标是.

查看解析收藏纠错

+选题
16. 二次函数 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 的最小值为1，则 $\text{[math]}$ 的取值范围是.

查看解析收藏纠错

+选题

17. 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ .

查看解析收藏纠错

+选题
18. 解分式方程： $\text{[math]}$ .

查看解析收藏纠错

+选题
19. 如图，在 $\text{[math]}$ 中，按以下步骤作图：

①以点 $\text{[math]}$ 为圆心，任意长为半径作弧，分别交边 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ；

②分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的相同长度为半径作弧，两弧交于点 $\text{[math]}$ ；

③作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ .

（1）根据上述步骤补全作图过程（要求：规作图，不写作法，保留作图痕迹）；

（2）如果 $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ 的面积与 $\text{[math]}$ 的面积的比值是.

查看解析收藏纠错

+选题
20. 如图，在足够大的空地上有一段长为 $\text{[math]}$ 的旧墙 $\text{[math]}$ ，某人利用旧墙和木栏围成一个矩形菜园 $\text{[math]}$ ，其中 $\text{[math]}$ .已知矩形菜园的一边靠墙，修筑另三边一共用了 $\text{[math]}$ 木栏.若所围成的矩形菜园的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题
21. 如图， $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ ，动点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ .求证： $\text{[math]}$ .

查看解析收藏纠错

+选题

22. 某公司生产某种产品，如果该产品年返修率不超过千分之一，则其生产部门当年考核优秀，现有该公司2012~2019年的相关数据如下表所示：

年份	2012	2013	2014	2015	2016	2017	2018	2019
年生产数量 $\text{[math]}$ 万台 $\text{[math]}$	2	3	4	5	6	7	10	11
该产品的年利润 $\text{[math]}$ 百万元 $\text{[math]}$	2.1	2.75	3.5	3.25	3	4.9	6	6.5
年返修数量/台	21	22	28	65	80	65	84	88
参考数据： $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ . 其中下角标1~8分别对应2012~2019年.

注：年返修率 $\text{[math]}$ .

（1）该公司的生产部门在2012~2019这八年中总共获得次考核优秀；

（2）从表中数据可以发现2016年的数据偏差较大，如果去掉2016年的数据，试用剩下的数据求出年利润 $\text{[math]}$ （百万元）的平均数.

查看解析收藏纠错

+选题

23. 模具厂计划生产面积为4，周长为m的矩形模具.对于m的取值范围，小亮已经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程如下：

（1）建立函数模型
设矩形相邻两边的长分别为x，y，由矩形的面积为4，得xy=4，即 $\text{[math]}$ ；由周长为m，得2（x+y）=m，即y=-x+ $\text{[math]}$ .满足要求的（x，y）应是两个函数图象在第象限内交点的坐标.

（2）画出函数图象
函数 $\text{[math]}$ （x＞0）的图象如图所示，而函数y=-x+ $\text{[math]}$ 的图象可由直线y=-x平移得到.请在同一直角坐标系中直接画出直线y=-x.

（3）平移直线y=-x，观察函数图象
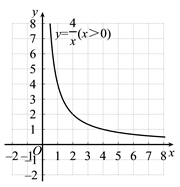
在直线平移过程中，交点个数有哪些情况？请写出交点个数及对应的周长m的取值范围.

（4）得出结论若能生产出面积为4的矩形模具，则周长m的取值范围为.

查看解析收藏纠错

+选题
24. 如图1， $\text{[math]}$ 的面积为1，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .设 $\text{[math]}$ ，图形 $\text{[math]}$ 的面积为 $\text{[math]}$ .

（1）如图2，当点 $\text{[math]}$ 和点 $\text{[math]}$ 重合时，求 $\text{[math]}$ 与 $\text{[math]}$ 的值；

（2）如图1，当点 $\text{[math]}$ 和点 $\text{[math]}$ 不重合时，求 $\text{[math]}$ 的最大值.

查看解析收藏纠错

+选题
25. 在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴， $\text{[math]}$ 轴分别交于 $\text{[math]}$ 、 $\text{[math]}$ 两点.抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ .

（1）如果抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，求该抛物线的解析式；

（2）如果抛物线 $\text{[math]}$ 的顶点 $\text{[math]}$ 位于 $\text{[math]}$ 内.
①求 $\text{[math]}$ 的取值范围；

②将该抛物线平移，平移后的抛物线仍经过点 $\text{[math]}$ ，此时点 $\text{[math]}$ 的对应点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，平移后的抛物线与线段 $\text{[math]}$ 是否还存在其它交点？若存在，请求出交点坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题

福建省2021年数学中考精准模拟试卷（三）

一、单选题

二、填空题

三、解答题

相关试卷收起∨

福建省2021年数学中考精准模拟试卷（三）

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨