重庆市九龙坡区2020-2021学年八年级上学期数学期末考试试卷

修改时间：2024-07-13 浏览次数：308 类型：期末考试编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 如果分式 $\text{[math]}$ 有意义，那么x的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列图案属于轴对称图形的是（　　）

A . B . C . D .

查看解析收藏纠错

+选题
3. 计算 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 观察下列图形，图（1）中有3个三角形，图（2）中有5个三角形，图（3）中有7个三角形，…若依此规律下去，则第5个图形中三角形的个数是（　　）

A . 9个 B . 11个 C . 13个 D . 15个

查看解析收藏纠错

+选题
5. 如果等腰三角形的两边长分别为7cm和3cm.那么它的第三边的长是（）

A . 3cm B . 4cm C . 7cm D . 3cm或7cm

查看解析收藏纠错

+选题
6. 在下列运算中，正确的是（）

A . （x﹣y）²＝x²﹣y² B . （a+2）（a﹣3）＝a²﹣6 C . （a+2b）²＝a²+4ab+4b² D . （2x﹣y）（2x+y）＝2x²﹣y²

查看解析收藏纠错

+选题
7. 如图，已知点A，D，C，F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（）

A . ∠BCA=∠F B . ∠B=∠E C . BC∥EF D . ∠A=∠EDF

查看解析收藏纠错

+选题
8. 如图，在△ABC中，∠ABC=50°，∠BAC=20°，D为线段AB的垂直平分线与直线BC的交点，连结AD，则∠CAD=（）

A . 40° B . 30° C . 20° D . 10°

查看解析收藏纠错

+选题
9. A，B两地相距48千米，一艘轮船从A地顺流航行至B地，又立即从B地逆流返回A地，共用去9小时，已知水流速度为4千米/时，若设该轮船在静水中的速度为x千米/时，则可列方程（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ +4=9 D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 数学课上，老师提出如下问题：
如图1，点P、Q是直线l同侧的两点，请你在直线l上确定一个点R.使 $\text{[math]}$ 的周长最小.小明的作法如下，如图2：

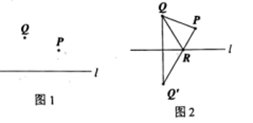
（ 1 ）作点Q关于直线l的对称点 $\text{[math]}$ ；

（ 2 ）连接 $\text{[math]}$ ，交直线l于点R；

（ 3 ）连接RQ、PQ.

那么点R就是使 $\text{[math]}$ 的周长最小的点.

老师说，小明的做法正确.接着.老师问同学们，小明这种作法应用了哪些我们学过的定理呢？有四位同学分别说了一个定理，下面的A，B，C，D四个答案分别代表了四个同学所说的定理，其中小明没有应用到的定理是（）

A . 如果两个图形关于某直线对称，那么对称轴是对称点连线的垂直平分线 B . 等腰三角形底边上的高也是顶角的角平分线 C . 线段垂直平分线上的点到线段两个端点的距离相等 D . 两点之间，线段最短

查看解析收藏纠错

+选题
11. 若关于x的分式方程 $\text{[math]}$ 有非负整数解，且关于y的不等式组 $\text{[math]}$ 有且只有2个整数解，则所有符合条件的正整数m的和为（）

A . 5 B . 7 C . 8 D . 9

查看解析收藏纠错

+选题
12. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，D是 $\text{[math]}$ 上的点，过点D作 $\text{[math]}$ 交 $\text{[math]}$ 于点F，交 $\text{[math]}$ 的延长线于点E，连接 $\text{[math]}$ ， $\text{[math]}$ .下列结论：① $\text{[math]}$ ：② $\text{[math]}$ ③ $\text{[math]}$ 是等边三角形：④若 $\text{[math]}$ ，则 $\text{[math]}$ .其中正确的是（　　）

A . ①②③ B . ①③④ C . ①②④ D . ②③④

查看解析收藏纠错

+选题

二、填空题

13. 计算 $\text{[math]}$ .

查看解析收藏纠错

+选题
14. 若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是．

查看解析收藏纠错

+选题
15. 约分： $\text{[math]}$ .

查看解析收藏纠错

+选题
16. 如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M、N，再分别以点M、N为圆心，大于 $\text{[math]}$ MN的长为半径画弧，两弧交于点P，作射线AP，交边BC于点D若CD=4，AB=15，则△ABD的面积是。

查看解析收藏纠错

+选题
17. 在平面直角坐标系中，已知点A（1，2），B（5，5），C（5，2），存在点E，使△ACE和△ACB全等，写出所有满足条件的E点的坐标．

查看解析收藏纠错

+选题
18. 如图所示，在等边三角形ABC中，AB边上的高 $\text{[math]}$ ，E是CD上一点，现有一动点Р沿着折线 $\text{[math]}$ 运动，在BE上的速度是每秒3个单位长度.在CE上的速度是每秒6个单位长度.则点Р从B到C的运动过程中最少需秒.

查看解析收藏纠错

+选题

三、解答题

19. 已知：如图，E是BC上一点，AB＝EC，AB∥CD，BC＝CD.求证：AC＝ED.

查看解析收藏纠错

+选题
20.

（1）因式分解： $\text{[math]}$ ；

（2）解方程： $\text{[math]}$

查看解析收藏纠错

+选题
21. 化简：

（1）（2a﹣b）²+（a+b）（a﹣b）

（2）（ $\text{[math]}$ a） $\text{[math]}$

查看解析收藏纠错

+选题
22. 如图，在等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D是 $\text{[math]}$ 边的中点， $\text{[math]}$ 交 $\text{[math]}$ 于点E，连接 $\text{[math]}$ .

（1）求 $\text{[math]}$ 的度数：

（2）求证： $\text{[math]}$ .

查看解析收藏纠错

+选题
23. 某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本，并按该书的定价7元出售，很快售完.由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用1500元所购该书数量比第一次多10本，并按该书的定价7元售出200本时，出现滞销，便以定价的4折售完剩余的书.

（1）第一次购书的批发价为每本多少元？

（2）该老板这两次售书总体上是赔钱了，还是赚钱了（不考虑其它因素）？若赔钱，赔多少？若赚钱，赚多少？

查看解析收藏纠错

+选题
24. 如图1是一个长为4a、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成的一个“回形”正方形（如图2）.

（1）图2中的阴影部分的面积为；

（2）观察图2请你写出（a+b）²、（a-b）²、ab之间的等量关系是；

（3）根据（2）中的结论，若x+y=7，xy= $\text{[math]}$ ，则x-y= ；

（4）实际上通过计算图形的面积可以探求相应的等式.根据图3，写出一个因式分解的等式 .

查看解析收藏纠错

+选题
25. 如图，等腰直角三角形ABC中， $\text{[math]}$ ， $\text{[math]}$ .

（1）如图1，等腰直角三角形ABC的顶点A在x轴的负半轴上，点B在y轴的负半轴上，且 $\text{[math]}$ ， $\text{[math]}$ ，求点C的坐标；

（2）如图2，等腰直角三角形ABC顶点A在y轴的负半轴上，点C在x轴的负半轴上，过点B作 $\text{[math]}$ 轴于点D，求证： $\text{[math]}$ ；

（3）如图3，点A的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 在y轴上运动，点 $\text{[math]}$ 在x轴上运动，在点B、C 的运动过程中，能否使得 $\text{[math]}$ 是一个以点A为直角顶点的等腰直角三角形，如果存在，请你直接写出m和n的数量关系；如果不存在，请说明理由.

查看解析收藏纠错

+选题
26. 在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE =∠BAC，连接CE.

（1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=度；

（2）设 $\text{[math]}$ ， $\text{[math]}$ .
①如图2，当点在线段BC上移动，则 $\text{[math]}$ ， $\text{[math]}$ 之间有怎样的数量关系？请说明理由；

②当点在直线BC上移动，则 $\text{[math]}$ ， $\text{[math]}$ 之间有怎样的数量关系？请直接写出你的结论.

查看解析收藏纠错

+选题

重庆市九龙坡区2020-2021学年八年级上学期数学期末考试试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨