修改时间：2021-05-20 浏览次数：1604 类型：中考真卷
小天、小东和小芸三位同学住在同一小区，该小区共有300户家庭，每户家庭人数在2﹣5之间，这300户家庭的平均人数均为3.4．
小天、小东和小芸各自对该小区家庭5月份用气量情况进行了抽样调查，将收集的数据进行了整理，绘制的统计表分别为表1，表2和表3．
表1 抽样调查小区4户家庭5月份用气量统计表 （单位：m3）
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2 抽样调查小区15户家庭5月份用气量统计表 （单位：m3）
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 20 | 22 |
表3 抽样调查小区15户家庭5月份用气量统计表 （单位：m3）
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 19 | 20 | 20 | 22 | 26 | 31 | 28 | 31 |
根据以上材料回答问题：
小天、小东和小芸三人中，哪一位同学抽样调查的数据能较好地反映该小区家庭5月份用气量情况，并简要说明其他两位同学抽样调查的不足之处．
北京市正围绕着“政治中心、文化中心、国际交往中心、科技创新中心”的定位，深入实施“人文北京、科技北京、绿色北京”的发展战略．“十二五”期间，北京市文化创意产业展现了良好的发展基础和巨大的发展潜力，已经成为首都经济增长的支柱产业．
2011年，北京市文化创意产业实现增加值1938.6亿元，占地区生产总值的12.2%.2012年，北京市文化创意产业继续呈现平稳发展态势，实现产业增加值2189.2亿元，占地区生产总值的12.3%，是第三产业中仅次于金融业、批发和零售业的第三大支柱产业.2013年，北京市文化产业实现增加值2406.7亿元，比上年增长9.1%，文化创意产业作为北京市支柱产业已经排到了第二位.2014年，北京市文化创意产业实现增加值2749.3亿元，占地区生产总值的13.1%，创历史新高，2015年，北京市文化创意产业发展总体平稳，实现产业增加值3072.3亿元，占地区生产总值的13.4%．
根据以上材料解答下列问题：
在等边△ABC中，
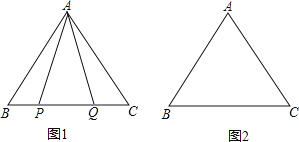
①依题意将图2补全；
②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：要证明PA=PM，只需证△APM是等边三角形；
想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；
想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…
请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．
试题篮
于点D，过点D作⊙O的切线，交BA的延长线于点E．
