初中数学苏科版八年级下册 7.4 频数分布表和频数分布直方图同步训练

1. 下列有关频数分布表和频数分布直方图的理解，正确的是（）

A . 频数分布表能清楚地反映事物的变化情况 B . 频数分布直方图能清楚地反映事物的变化情况 C . 频数分布直方图能清楚地表示出各部分在总体中所占的百分比 D . 二者均不能清楚地反映变化情况和在总体中所占的百分比，但能反映出每个项目的具体数目

查看解析收藏纠错

+选题
2. 某班将安全知识竞赛成绩整理后绘制成直方图，图中从左至右前四组的百分比分别是4%、12%、40%、28%，第五组的频数是8，下列结论错误的是（）

A . 80分以上的学生有14名 B . 该班有50名同学参赛 C . 成绩在70～80分的人数最多 D . 第五组的百分比为16%

查看解析收藏纠错

+选题
3. 某校为了了解学生在校午餐所需的时间，抽查了 20 名同学在校午餐所需的时间，获得如下数据（单位：分）：10，12，15，10，16，18，19，18，20，34，22，25，20，18，18，20，15，16，21，16.若将这些数据分为 5组，则组距是（）

A . 4 分 B . 5 分 C . 6 分 D . 7 分

查看解析收藏纠错

+选题
4. 为了了解本校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图，则仰卧起坐次数在25次（含25次）以上的人数共有（）

A . 10人 B . 12人 C . 17人 D . 都不对

查看解析收藏纠错

+选题
5. 为了了解某校七年级学生的体能情况，随机调查了其中100名学生，测试学生在1分钟内跳绳的次数，并绘制成如图所示的频数分布直方图 $\text{[math]}$ 请根据图形计算，跳绳次数 $\text{[math]}$ 在 $\text{[math]}$ 范围内人数占抽查学生总人数的百分比为 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 学校为了解七年级学生参加课外兴趣小组活动情况，随机调查了40名学生，将结果绘制成了如图所示的频数分布直方图，则参加绘画兴趣小组的频率是（）

A . 0.1 B . 0.15 C . 0.25 D . 0.3

查看解析收藏纠错

+选题
7. 为了了解噪声污染的情况，某市环保局抽样调查了80个测量点的噪声声级(单位：分贝)，并进行整理后分成五组，绘制出频数分布直方图，如图所示．已知从左至右前四组的频率分别是0.15，0.25，0.3，0.2，且噪声声级高于69.5分贝就会影响工作和生活，那么影响到工作和生活而需对附近区域进行治理的测量点有（）

A . 5个 B . 8个 C . 12个 D . 15个

查看解析收藏纠错

+选题
8. 某班50名学生期末考试数学成绩（单位：分）的频率分布直方图如图所示，其中
数据不在分点上，对图中提供的信息作出如下的判断：
②成绩在79.5～89.5分段的人数占30%；
③成绩在79.5分以上的学生有20人；
④本次考试成绩的中位数落在69.5～79.5分段内．
其中正确的判断有（）

A . 4个 B . 3个 C . 2个 D . 1个

查看解析收藏纠错

+选题
9. 小聪对他所在小区居民每天微信阅读时间进行了抽样调查，并绘制成了如图所示的统计图．根据图中信息，其中正确的是（　　）
①小聪一共抽样调查了60人

②每天微信阅读时间多于50分钟的人数有12人

③每天微信阅读时间30~40分钟的人数最多

④每天微信阅读时间不足30分钟的人数多于调查总人数的一半

A . ①② B . ②③ C . ②④ D . ③④

查看解析收藏纠错

+选题
10. 小明统计了同学们5月份平均每天观看北京市“空中课堂”的时间，并绘制了统计图，如图所示下面有四个推断

①此次调查中，小明一共调查了100名学生

②此次调查中，平均每天观看时间不足30分钟的人数占总人数的10%

③此次调查中，平均每天观看时间超过60分钟的人数超过调查总人数的一半

④此次调查中，平均每天观看时间不足60分钟的人数少于平均每天观看时间在60-90分钟的人数

所有合理推断的序号是（）

A . ①② B . ①④ C . ③④ D . ②③④

查看解析收藏纠错

+选题

11. 某校701班数学期终考试全班所有学生成绩的频数分布直方图如图所示，满分100分，学生成绩取整数，则成绩在90.5~95.5这一分数段的频率是。

查看解析收藏纠错

+选题
12. 江涛同学统计了他家10月份的长途电话明细清单，按通话时间画出直方图如图，则他家这个月打了长途电话的次数一共是．

查看解析收藏纠错

+选题
13. 如图是某班45个学生在一次数学测试中成绩的频数分布直方图（成绩为整数），图中从左到右的小长方形的高度比为1：3：5：4：2，则该次数学测试成绩在80.5到90.5之间的学生有个．

查看解析收藏纠错

+选题
14. 抽取某校学生一个容量为150的样本，测得学生身高后，得到身高频数分布直方图如图，已知该校有学生1500人，则可以估计出该校身高位于160 cm和165 cm之间的学生大约有人.

查看解析收藏纠错

+选题
15. 为了解某校九年级女生1分钟仰卧起坐的次数，从中随机抽查了50名女生参加测试，被抽查的女生中有90%的女生次数不小于30次，并绘制成频数分布直方图（如图），那么仰卧起坐的次数在40～45的频率是．

查看解析收藏纠错

+选题
16. 某校在“数学小论文“评比活动中，共征集到论文100篇，对论文评比的分数(分数为整数)整理后，分组画出频数分布直方图(如图)，已知从左到右5个小长方形的高的比为1：3：7：6：3，那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有篇.

查看解析收藏纠错

+选题
17. 某学校初二年级进行“垃圾分类，从我做起”垃圾分类知识竞赛活动，并对测试成绩进行了分组整理，各分数段的人数如图所示（满分100分）．

请观察统计图，填空并回答下列问题：

（1）这个学校初二年级共有名学生；

（2）成绩在分数段的人数最多、最集中，占全年级总人数的比值是；

（3）若从该年级随意找出一名学生，他的测试成绩在分数段的可能性最小，可能性是．

查看解析收藏纠错

+选题
18. 为响应“红歌唱响中国”活动，某乡镇举行了一场“红歌”歌咏比赛，组委会规定：任何一名参赛选手的成绩x满足：60≤x＜100，赛后整理所有参赛选手的成绩如下表：
分数段
频数
频率
60≤x＜70
30
0.15
70≤x＜80
m
0.45
80≤x＜90
60
n
90≤x＜100
20
0.1
根据表中提供的信息得到 m= ,n＝.

查看解析收藏纠错

+选题

19.
第一次模拟考试后，数学科陈老师把一班的数学成绩制成如图的统计图（图中每组数据包含横轴上左边的数据不含右边的数据），并给了几个信息：①前两组的频率和是0.14；②第一组的频率是0.02；③自左到右第二、三、四组的频数比为3：9：8．
请结合统计图完成下列问题：
（1）这个班学生是多少人？
（2）成绩不少于90分为优秀，那么这个班成绩的优秀率是多少？

查看解析收藏纠错

+选题
20. 疫情期间，松桃县某中学八（1）班学生积极观看“空中黔课”，数学老师对第一章的学习效果检测成绩进行统计分析，发现达到优秀（80分及以上）的频率为0.3，各分数段的人数如图所示（分数取正整数，满分100分），请观察图形，并回答下列问题：

（1）该班共有多少名学生？

（2）求出 $\text{[math]}$ 这一组的人数，并补全频数分布直方图.

查看解析收藏纠错

+选题
21.
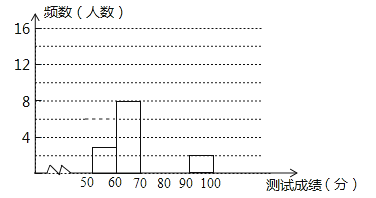
为了增强学生环保意识，我区举办了首届“环保知识大赛”，经选拔后有30名学生参加决赛，这30，名学生同事解答50个选择题，若每正确一个选择题得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
组别
成绩x分
频数（人数）
第1组
50≤x＜60
3
第2组
60≤x＜70
8
第3组
70≤x＜80
13
第4组
80≤x＜90
a
第5组
90≤x＜100
2
（1）求表中a的值；
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？
（4）第4组的同学将抽出3名对第一组3名同学进行“一帮一”辅导，则第4组的小宇与小强能同时抽到的概率是多少？

查看解析收藏纠错

+选题
22.
统计七年级若干名学生的跳高测试成绩，得到如图所示的频数分布直方图（每组数据含最小值，不含最大值）．请回答下列问题：
（1）参加测试的总人数有多少人？若规定跳高高度超过1.09米为达标，则此次跳高达标率为多少？（精确到1%）
（2）数据分组的组距是多少？
（3）频数最大的一组的频率是多少（精确到0.01）？该组的两个边界值分别是多少？

查看解析收藏纠错

+选题

23. 某校为了解八年级学生的视力情况，对八年级的学生进行了一次视力调查，并将调查数据进行统计整理，绘制出如下频数分布表和频数分布直方图的一部分．

视力	频数/人	频率
4.0≤x＜4.3	20	0.1
4.3≤x＜4.6	40	0.2
4.6≤x＜4.9	70	0.35
4.9≤x＜5.2	a	0.3
5.2≤x＜5.5	10	b

（1）在频数分布表中，a＝，b＝；

（2）将频数分布直方图补充完整；

（3）若视力在4.6以上(含4.6)均属正常，求视力正常的人数占被调查人数的百分比．

查看解析收藏纠错

+选题

24. 我市提倡“诵读中华经典，营造书香校园”的良好诵读氛围，促进校园文化建设，进而培养学生的良好诵读习惯，使经典之风浸漫校园．某中学为了了解学生每周在校经典诵读时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表，请根据图表信息解答下列问题：

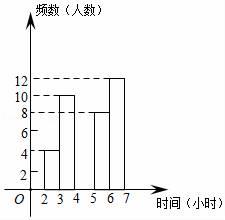
时间（小时）	频数（人数）	频率
2≤t＜3	4	0.1
3≤t＜4	10	0.25
4≤t＜5	a	0.15
5≤t＜6	8	b
6≤t＜7	12	0.3
合计	40	1

（1）表中的a＝，b＝；

（2）请将频数分布直方图补全；

（3）若该校共有1200名学生，试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名？

查看解析收藏纠错

+选题

25. 垃圾分类是对垃圾传统收集处理方式的改变，是对垃圾进行有效处理的一种科学管理方法为了增强同学们垃圾分类的意识，某校举行一场学生在线参与垃圾分类处理知识测试（满分100分，得分均为整数）.学校从全校1200名学生中随机抽取部分学生的成绩，绘制成如下不完整的统计图表.抽取的部分学生测试成绩的频数分布表

成绩 $\text{[math]}$ （分）	频数（人）	百分比
$\text{[math]}$	10	$\text{[math]}$
$\text{[math]}$	15	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	40	$\text{[math]}$
$\text{[math]}$	15	$\text{[math]}$