北京市第四中学2020-2021学年八年级上学期数学期中试卷

修改时间：2024-07-31 浏览次数：174 类型：期中考试编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 下列轴对称图形中，有4条对称轴的图形是（）

A . B . C . D .

查看解析收藏纠错

+选题
2. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 下列变形属于因式分解的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 在平面直角坐标系上，已知点A关于直线x＝1对称的点为B（﹣2，4），则点A的坐标为（）

A . （4，4） B . （﹣2，﹣2） C . （2，4） D . （3，4）

查看解析收藏纠错

+选题
5. 电子文件的大小常用 $\text{[math]}$ 等作为单位，其中 $\text{[math]}$ ，某视频文件的大小约为 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 已知 $\text{[math]}$ ，则a²+4b²的值是（）

A . 110 B . 120 C . 125 D . 130

查看解析收藏纠错

+选题
7. 图（1）是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（）

A . B . $\text{[math]}$ C . D .

查看解析收藏纠错

+选题
8. 如图所示，三角形纸片被正方形纸板遮住了一部分，小明根据所学知识画出了一个与该三角形完全重合的三角形，那么这两个三角形完全重合的依据是（）

A . SSS B . SAS C . AAS D . ASA

查看解析收藏纠错

+选题
9. 我们利用尺规作图可以作一个角 $\text{[math]}$ 等于已知角 $\text{[math]}$ ，如下所示：

（1）作射线 $\text{[math]}$ ；（2）以 $\text{[math]}$ 为圆心，任意长为半径作弧，交 $\text{[math]}$ 于 $\text{[math]}$ ，交 $\text{[math]}$ 于 $\text{[math]}$ ；（3）以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作弧，交 $\text{[math]}$ 于 $\text{[math]}$ ；（4）以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作弧，交前面的弧于 $\text{[math]}$ ；（5）连接 $\text{[math]}$ 作射线 $\text{[math]}$ 则 $\text{[math]}$ 就是所求作的角．

以上作法中，错误的一步是（）

A . （2） B . （3） C . （4） D . （5）

查看解析收藏纠错

+选题
10. △BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道（）

A . △ABC的周长 B . △AFH的周长 C . 四边形FBGH的周长 D . 四边形ADEC的周长

查看解析收藏纠错

+选题

二、填空题

11. 分解因式： $\text{[math]}$ ．

查看解析收藏纠错

+选题
12. 在正方形网格中， $\text{[math]}$ 的位置如图所示，则点 $\text{[math]}$ 中在 $\text{[math]}$ 的平分线上是点．

查看解析收藏纠错

+选题
13. 若3x+2y﹣2=0，则 $\text{[math]}$ 等于．

查看解析收藏纠错

+选题
14. 如图，在△ABC中，点D在BC上，将点D分别以AB、AC为对称轴，画出对称点E、F，并连接AE、AF.根据图中标示的角度，则∠EAF=°.

查看解析收藏纠错

+选题

15. 已知关于 $\text{[math]}$ 的代数式 $\text{[math]}$ ，设代数式的值为 $\text{[math]}$ ，则 $\text{[math]}$ ．下表中列出了当 $\text{[math]}$ 分别取…， $\text{[math]}$ …， $\text{[math]}$ …时对应的 $\text{[math]}$ 值．

$\text{[math]}$	···	-1	0	1	2	3	4	5	···	$\text{[math]}$	$\text{[math]}$	···
$\text{[math]}$	···	10	5	2	1	2	5	$\text{[math]}$	···	$\text{[math]}$	$\text{[math]}$	···

（1）表中n的值为；

（2）当 $\text{[math]}$ 时， $\text{[math]}$ 有最小值，最小值是；

（3） $\text{[math]}$ $\text{[math]}$ ．（填 $\text{[math]}$ ）

查看解析收藏纠错

+选题

16. 已知等腰三角形一个外角的度数为108°，则顶角度数为.

查看解析收藏纠错

+选题
17. 已知锐角 $\text{[math]}$ 如图

⑴在射线 $\text{[math]}$ 上取一点 $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径作弧 $\text{[math]}$ ，交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ；

⑵分别以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径作弧，两弧交于点 $\text{[math]}$ 连接 $\text{[math]}$ ；

⑶作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．

根据以上作图过程及所作图形，下列结论中正确的是；

$\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$

查看解析收藏纠错

+选题
18. 如图，已知每个小方格的边长为 $\text{[math]}$ 两点都在小方格的顶点上（即为格点），请在图中找一个格点 $\text{[math]}$ ，使 $\text{[math]}$ 为等腰三角形，则这样的格点 $\text{[math]}$ 有个．

查看解析收藏纠错

+选题
19. 若 $\text{[math]}$ 为正奇数，则 $\text{[math]}$ (底数中含k个k)；若 $\text{[math]}$ 为正偶数，则 $\text{[math]}$ (底数中含k个k)；

查看解析收藏纠错

+选题
20. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为a，小正方形地砖面积为依次连接四块大正方形地砖的中心得到正方形ABCD．则正方形ABCD的面积为（用含a，b的代数式表示）．

查看解析收藏纠错

+选题

三、解答题

21. 分解因式：

（1） $\text{[math]}$ ；

（2） $\text{[math]}$ ．

查看解析收藏纠错

+选题
22. 计算：

（1） $\text{[math]}$

（2） $\text{[math]}$ ；

（3） $\text{[math]}$ ；

（4） $\text{[math]}$ ．

查看解析收藏纠错

+选题
23. 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$

查看解析收藏纠错

+选题
24. 如图， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ．

查看解析收藏纠错

+选题
25. 小宇遇到了这样一个问题：
已知：如图， $\text{[math]}$ ，点A，B分别在射线OM，ON上，且满足 $\text{[math]}$ ．

求作：线段OB上的一点C，使 $\text{[math]}$ 的周长等于线段 $\text{[math]}$ 的长．

以下是小宇分析和求解的过程，请补充完整：首先画草图进行分析，如图1所示，若符合题意得点C已经找到，即 $\text{[math]}$ 得周长等于OB的长，那么由 $\text{[math]}$ ，可以得到 $\text{[math]}$ ．

对于这个式子，可以考虑用截长得办法，在BC上取一点D，使得 $\text{[math]}$ ，那么就可以得到 $\text{[math]}$ ．

若连接AD，由．（填推理依据）．可知点C在线段AD得垂直平分线上，于是问题得解法就找到了．

请根据小宇得分析，在图2中完成作图（尺规作图，不写做法，保留作图痕迹）．

查看解析收藏纠错

+选题
26. 阅读材料
小明遇到这样一个问题：求计算 $\text{[math]}$ 所得多项式的一次项系数.

小明想通过计算 $\text{[math]}$ 所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法.

他决定从简单情况开始，先找 $\text{[math]}$ 所得多项式中的一次项系数，通过观察发现：

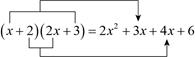
也就是说，只需用 $\text{[math]}$ 中的一次项系数1乘以 $\text{[math]}$ 中的常数项3，再用 $\text{[math]}$ 中的常数项2乘以 $\text{[math]}$ 中的一次项系数2，两个积相加 $\text{[math]}$ ，即可得到一次项系数.

延续上面的方法，求计算 $\text{[math]}$ 所得多项式的一次项系数，可以先用 $\text{[math]}$ 的一次项系数1， $\text{[math]}$ 的常数项3， $\text{[math]}$ 的常数项4，相乘得到12；再用 $\text{[math]}$ 的一次项系数2， $\text{[math]}$ 的常数项2， $\text{[math]}$ 的常数项4，相乘得到16；然后用 $\text{[math]}$ 的一次项系数3， $\text{[math]}$ 的常数项2 $\text{[math]}$ 的常数项3，相乘得到18.最后将12，16，18相加，得到的一次项系数为46.

参考小明思考问题的方法，解决下列问题：

（1）计算 $\text{[math]}$ 所得多项式的一次项系数为.

（2）计算 $\text{[math]}$ 所得多项式的一次项系数为.

（3）若 $\text{[math]}$ 是 $\text{[math]}$ 的一个因式，求 $\text{[math]}$ 、 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
27. 如图1，点 $\text{[math]}$ 是等腰三角形 $\text{[math]}$ 外一点， $\text{[math]}$ 过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ．

（1）依据题意，补全图形．

（2）求证： $\text{[math]}$ ．

（3）如图2， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，当 $\text{[math]}$ 是 $\text{[math]}$ 的中点时，翻折 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ 求证： $\text{[math]}$ 两点到直线 $\text{[math]}$ 的距离相等．

查看解析收藏纠错

+选题

28. 小明同学研究如下问题：

从 $\text{[math]}$ ，…， $\text{[math]}$ 为整数，且 $\text{[math]}$ ）这 $\text{[math]}$ 个整数中任取 $\text{[math]}$ 个整数，这 $\text{[math]}$ 个整数之和共有多少种不同的结果？

他采取一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，从中找出解决问题的方法．他进行了如下几个探究：

（1）探究一：

从 $\text{[math]}$ 这3个整数中任取2个整数，这2个整数之和共有多少种不同的结果？

所取的2个整数	1，2	1，3	2，3
2个整数之和	3	4	5

如上表，所取的2个整数之和可以为 $\text{[math]}$ ，也就是从3到5的连续整数，其中最小是3最大是5所以共有3种不同的结果．

（2）从 $\text{[math]}$ 这4个整数中任取2个整数，这2个整数之和共有多少种不同的结果？

所取的2个整数	1，2	1，3	1，4	2，3	2，4	3，4
2个整数之和	3	4	5	5	6	4

如上表，所取的2个整数之和可以为 $\text{[math]}$ ，也就是从3到7的连续整数，其中最小是3，最大是7，所以共有5种不同的结果．

（3）从 $\text{[math]}$ 这 $\text{[math]}$ 个整数中任取 $\text{[math]}$ 个整数，这 $\text{[math]}$ 个整数之和共有_种不同的结果．

（4）从 $\text{[math]}$ ，…， $\text{[math]}$ 为整数，且 $\text{[math]}$ ）这 $\text{[math]}$ 个整数中任取 $\text{[math]}$ 个整数，这 $\text{[math]}$ 个整数之和共有__种不同的结果．

（5）探究二：从 $\text{[math]}$ 这 $\text{[math]}$ 个整数中任取 $\text{[math]}$ 个整数，这 $\text{[math]}$ 个整数之和共有种不同的结果．

（6）从 $\text{[math]}$ ，…， $\text{[math]}$ 为整数，且 $\text{[math]}$ ）这 $\text{[math]}$ 个整数中任取 $\text{[math]}$ 个整数，这 $\text{[math]}$ 个整数之和共有种不同的结果．

（7）探究三：从 $\text{[math]}$ ，…， $\text{[math]}$ 为整数，且 $\text{[math]}$ 这 $\text{[math]}$ 个整数中任取 $\text{[math]}$ 个整数，这 $\text{[math]}$ 个整数之和共有种不同的结果．

归纳结论：从 $\text{[math]}$ ，…， $\text{[math]}$ 为整数，且 $\text{[math]}$ 这 $\text{[math]}$ 个整数中任取 $\text{[math]}$ 个整数，这 $\text{[math]}$ 个整数之和共有种不同的结果．

拓展延伸：从 $\text{[math]}$ ，…， $\text{[math]}$ 这 $\text{[math]}$ 个整数中任取个整数，使得取出的这些整数之和共有 $\text{[math]}$ 种不同的结果？（写出解答过程）

查看解析收藏纠错

+选题

29. 如图， $\text{[math]}$ 中， $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到点 $\text{[math]}$ ，点 $\text{[math]}$ 与点 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称，连接 $\text{[math]}$ ．

（1）依题意补全图形；

（2）判断 $\text{[math]}$ 的形状，并证明；

（3）请问在直线 $\text{[math]}$ 上是否存在点 $\text{[math]}$ ，使得 $\text{[math]}$ 成立？若存在，请用文字描述出点 $\text{[math]}$ 的准确位置，并画图证明：若不存在，请说明理由．

查看解析收藏纠错

+选题

北京市第四中学2020-2021学年八年级上学期数学期中试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨