北京市房山区2019-2020学年八年级下学期数学期末试卷

1. 一元二次方程x²﹣4x﹣3＝0的二次项系数、一次项系数和常数项分别是（）

A . 1，4，3 B . 0，﹣4，﹣3 C . 1，﹣4，3 D . 1，﹣4，﹣3

查看解析收藏纠错

+选题
2. 下面四个高校校徽主体图案是中心对称图形的是（）

A . 北京大学 B . 中国人民大学 C . 北京体育大学 D . 北京林业大学

查看解析收藏纠错

+选题
3. 函数 $\text{[math]}$ 的自变量x的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 点(﹣2，5)关于坐标原点对称的点的坐标是（）

A . (2，﹣5) B . (﹣2，﹣5) C . (2，5) D . (5，﹣2)

查看解析收藏纠错

+选题
5. 四边形的外角和为（）

A . 180° B . 360° C . 540° D . 720°

查看解析收藏纠错

+选题

6. 某区学生在“垃圾分类知识”线上答题活动中，甲、乙、丙、丁四所学校参加线上答题的人数相同，四所学校答题所得分数的平均数和方差的数值如表：

选手	甲	乙	丙	丁
平均数	87	87	87	87
方差	0.027	0.043	0.036	0.029

则这四所学校成绩发挥最稳定的是（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题

7. 方程x²﹣3x＝0的根是（）

A . x＝0 B . x＝3 C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，在 $\text{[math]}$ 中，AE平分∠BAD，交CD边于E，AD＝6，EC＝4，则AB的长为（）

A . 1 B . 6 C . 10 D . 12

查看解析收藏纠错

+选题
9. 某家快递公司今年一月份完成投递的快递总件数为30万件，三月份完成投递的快递总件数为36.3万件，若每月投递的快递总件数的增长率x相同，则根据题意列出方程为（）

A . 30（2x+1）＝36.3 B . 30（x+1）²＝36.3 C . 30（2x﹣1）＝36.3 D . 30（x﹣1）²＝36.3

查看解析收藏纠错

+选题
10. 如图，在长方形ABCD中，AB＝2，BC＝1，运点P从点B出发，沿路线B→C→D作匀速运动，那么△ABP的面积y与点P运动的路程x之间的函数图象大致是（）.

A . B . C . D .

查看解析收藏纠错

+选题

11. 若点M的坐标为（1，﹣1），则点M在第象限．

查看解析收藏纠错

+选题
12. 贝贝在练习“投掷铅球”项目活动中进行了5次测试，测试成绩（单位：分）如下：10，7，9，4，10．则贝贝5次成绩的极差是．

查看解析收藏纠错

+选题
13. 将一次函数 $\text{[math]}$ 的图象向上平移2个单位长度，所得的函数解析式为.

查看解析收藏纠错

+选题
14. 如图，A，B两地被池塘隔开，小明通过下面的方法测出A，B间的距离：先在AB外选一点C，连接AC，BC，分别取AC，BC的中点D，E，测得DE＝15米，由此他知道了A，B间的距离为米．

查看解析收藏纠错

+选题
15. 如图是天安门广场周围的景点分布示意图．在图中，分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系．若表示故宫的点的坐标为（0，0），则表示人民大会堂的点的坐标为．

查看解析收藏纠错

+选题
16. 正方形ABCD的边长为1，点P为对角线AC上任意一点，PE⊥AD，PF⊥CD，垂足分别是E，F．则PE+PF＝．

查看解析收藏纠错

+选题
17. 若关于x的一元二次方程（a+3）x²+2x+a²﹣9＝0有一个根为0，则a的值为．

查看解析收藏纠错

+选题
18. 在四边形ABCD中，有以下四个条件：①AB∥CD；②AD＝BC；③AC＝BD；④∠ADC＝∠ABC．从中选取三个条件，可以判定四边形ABCD为矩形．则可以选择的条件序号是．

查看解析收藏纠错

+选题

19. 解方程：（x﹣1）²=4．

查看解析收藏纠错

+选题
20. 解方程：x²+3x﹣1＝0．

查看解析收藏纠错

+选题
21. 已知：△ABC，画一个平行四边形ABCD，使AB，BC为邻边，AC为对角线，并说明画图依据。

查看解析收藏纠错

+选题
22. 已知一次函数的图象经过(1，3)和(﹣1，7)两点．

（1）求这个一次函数的表达式；

（2）求这个一次函数与坐标轴所围成的三角形的面积．

查看解析收藏纠错

+选题
23. 如图，在▱ABCD中，点M，N分别是边AB，CD的中点．
求证：AN=CM．

查看解析收藏纠错

+选题
24. 关于x的一元二次方程x²﹣2x+2m﹣1＝0有实数根．

（1）求m的取值范围；

（2）请选择一个符合条件的m的值，并求此时方程的根．

查看解析收藏纠错

+选题

25. 为了进一步推进“书香房山”建设，2020年4月房山区启动2020年“书香中国·北京阅读季”全民阅读活动．在一个月的活动中随机调查了某校八年级学生的周人均阅读时间的情况，整理并绘制了如下的统计图表：

某校八年级学生周人均阅读时间频数分布表

周人均阅读时间x（小时）	频数	频率
0≤x＜2	5	0.025
2≤x＜4	30	0.150
4≤x＜6	a	0.200
6≤x＜8	55	0.275
8≤x＜10	50	0.250
10≤x＜12	20	b
合计	200	1.000

请根据以上信息，解答下列问题：

（1）在频数分布表中a＝，b＝；

（2）补全频数分布直方图；

（3）若该校有1000名学生，根据调查数据，请你估计该校学生周人均阅读时间不少于6小时的学生大约有人．

查看解析收藏纠错

+选题

26. 已知：如图，在四边形ABCD中，AC为对角线，AD∥BC，BC＝2AD，∠BAC＝90°，过点A作AE∥DC交BC于点E．

（1）求证：四边形AECD为菱形；

（2）若AB＝AE＝2，求四边形AECD的面积．

查看解析收藏纠错

+选题

27. 有这样一个问题：探究函数 $\text{[math]}$ 的图象与性质．下面是小艺的探究过程，请补充完整：

（1）函数 $\text{[math]}$ 的自变量x的取值范围是；

（2）下表是y与x的几组对应值．

x	…	﹣2	﹣1	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1	2	…
y	…	$\text{[math]}$		$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	2		…

补全表格中的数据，并画出该函数的图象．

（3）请写出该函数的一条性质：．

查看解析收藏纠错

+选题

28. 在平面直角坐标系xOy中，对于任意三点A，B，C的“矩积”，给出如下定义：“横底”a：任意两点横坐标差的最大值；“纵高”h：任意两点纵坐标差的最大值；则“矩积”S＝ah．例如：三点坐标分别为A（1，﹣2），B（2，2），C（﹣1，﹣3），则“横底”a＝3，“纵高”h＝5，“矩积”S＝ah＝15．已知点D（﹣2，3），E（1，﹣1）．

（1）若点F在x轴上．
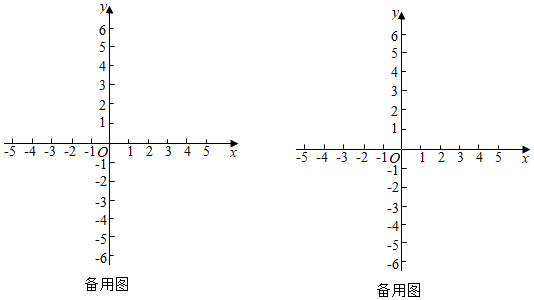
①当D，E，F三点的“矩积”为24，则点F的坐标为；

②直接写出D，E，F三点的“矩积”的最小值为；

（2）若点F在直线y＝mx+4上，使得D，E，F三点的“矩积”取到最小值，直接写出m的取值范围是．

查看解析收藏纠错

+选题

北京市房山区2019-2020学年八年级下学期数学期末试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

北京市房山区2019-2020学年八年级下学期数学期末试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨