解直角三角形的应用专题训练

修改时间：2020-07-08 浏览次数：306 类型：二轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、综合题

1. 有一种升降熨烫台如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图，AB和CD是两根相同长度的活动支撑杆，点O是它们的连接点，OA＝OC，h(cm)表示熨烫台的高度.

（1）如图2—1，若AB＝CD＝110cm，∠AOC＝120°，求h的值；

（2）爱动脑筋的小明发现，当家里这种升降熨烫台的高度为120cm时，两根支撑杆的夹角∠AOC是74°（如图2—2），求该熨烫台支撑杆AB的长度（结果精确到1cm）.（参考数据：sin37°≈0.6，cos37°≈0.8，sin53°≈0.8，cos53°≈0. 6）

查看解析收藏纠错

+选题

2. 为了测量一条两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向。测量方案与数据如下表：

课题	测量河流宽度
测量工具	测量角度的仪器，皮尺等
测量小组	第一小组	第二小组	第三小组
测量方案示意图
说明	点B，C在点A的正东方向	点B，D在点A的正东方向	点B在点A的正东方向，点C在点A的正西方向
测量数据	BC=60m， ∠ABH=70°， ∠ACH=35°	BD=20m， ∠ABH=70°， ∠BCD=35°	BC=101m， ∠ABH=70°， ∠ACH=35°

(参考数据：sin70°≈0.94，sin35°≈0.57，tan70°≈2.75，tan35°≈0.70)

（1）哪个小组的数据无法计算出河宽？

（2）请选择其中一个方案及其数据求出河宽(精确到0.1m)。

查看解析收藏纠错

+选题

3. 第二届“一带一路”国际合作高峰论坛将于2019年4月在北京举行．为了让恩施特产走出大山，走向世界，恩施一民营企业计划生产甲、乙两种商品共10万件，销住“一带一路”沿线国家和地区．已知3件甲种商品与2件乙种商品的销售收入相同，1件甲种商品比2件乙种商品的销售收入少600元．甲、乙两种商品的销售利润分别为120元和200元

（1）甲、乙两种商品的销售单价各多少元？

（2）市场调研表明：所有商品能全部售出，企业要求生产乙种商品的数量不超过甲种商品数量的 $\text{[math]}$ ，且甲、乙两种商品的销售总收入不低于3300万元，请你为该企业设计一种生产方案，使销售总利润最大．

查看解析收藏纠错

+选题
4. 【材料阅读】
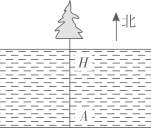
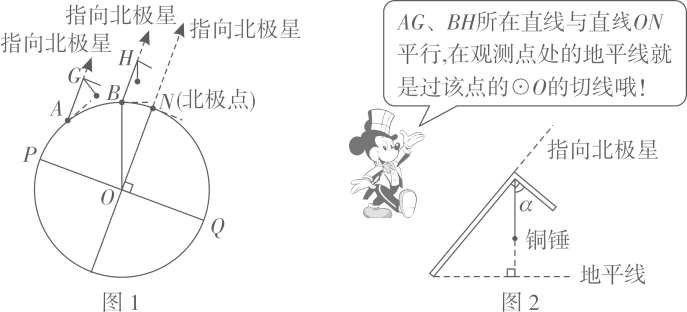
地球是一个球体，任意两条相对的子午线都组成一个经线圈（如图 $\text{[math]}$ 中的 $\text{[math]}$ ）.人们在北半球可观测到北极星，我国古人在观测北极星的过程中发明了如图 $\text{[math]}$ 所示的工具尺（古人称它为“复矩”），尺的两边互相垂直，角顶系有一段棉线，棉线末端系一个铜锤，这样棉线就与地平线垂直.站在不同的观测点，当工具尺的长边指向北极星时，短边与棉线的夹角 $\text{[math]}$ 的大小是变化的.

【实际应用】观测点 $\text{[math]}$ 在图1所示的 $\text{[math]}$ 上，现在利用这个工具尺在点 $\text{[math]}$ 处测得 $\text{[math]}$ 为 $\text{[math]}$ ，在点 $\text{[math]}$ 所在子午线往北的另一个观测点 $\text{[math]}$ ，用同样的工具尺测得 $\text{[math]}$ 为 $\text{[math]}$ . $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ .

（1）求 $\text{[math]}$ 的度数；

（2）已知 $\text{[math]}$ km，求这两个观测点之间的距离即 $\text{[math]}$ 上 $\text{[math]}$ 的长.（ $\text{[math]}$ 取 $\text{[math]}$ ）

查看解析收藏纠错

+选题
5. 小李要外出参加“建国70周年”庆祝活动，需网购一个拉杆箱，图①，②分别是她上网时看到的某种型号拉杆箱的实物图与示意图，并获得了如下信息：滑杆 $\text{[math]}$ ，箱长 $\text{[math]}$ ，拉杆 $\text{[math]}$ 的长度都相等， $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 在 $\text{[math]}$ 上，支杆 $\text{[math]}$ $\text{[math]}$ ，请根据以上信息，解决下列向题.

（1）求 $\text{[math]}$ 的长度（结果保留根号）；

（2）求拉杆端点 $\text{[math]}$ 到水平滑杆 $\text{[math]}$ 的距离（结果保留根号）.

查看解析收藏纠错

+选题
6. 在一次海上救援中，两艘专业救助船 $\text{[math]}$ 同时收到某事故渔船的求救讯息，已知此时救助船 $\text{[math]}$ 在 $\text{[math]}$ 的正北方向，事故渔船 $\text{[math]}$ 在救助船 $\text{[math]}$ 的北偏西30°方向上，在救助船 $\text{[math]}$ 的西南方向上，且事故渔船 $\text{[math]}$ 与救助船 $\text{[math]}$ 相距120海里.

（1）求收到求救讯息时事故渔船 $\text{[math]}$ 与救助船 $\text{[math]}$ 之间的距离；

（2）若救助船A ， $\text{[math]}$ 分别以40海里/小时、30海里/小时的速度同时出发，匀速直线前往事故渔船 $\text{[math]}$ 处搜救，试通过计算判断哪艘船先到达.

查看解析收藏纠错

+选题
7. 如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图，图中OP为下水管道口直径，OB为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开，可排出城市污水；当河水上涨时，阀门会因河水压迫而关闭，以防河水倒灌入城中.若阀门的直径OB＝OP＝100cm，OA为检修时阀门开启的位置，且OA＝OB.
（ $\text{[math]}$ ＝1.41，sin67.5°＝0.92，cos67.5°＝0.38，tan67.5°＝2.41，sin22.5°＝0.38，cos22.5°＝0.92，tan22.5°＝0.41）

（1）直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围；

（2）为了观测水位，当下水道的水冲开阀门到达OB位置时，在点A处测得俯角∠CAB＝67.5°，若此时点B恰好与下水道的水平面齐平，求此时下水道内水的深度.（结果保留小数点后一位）

查看解析收藏纠错

+选题
8. 如图，海中有两个小岛 $\text{[math]}$ ， $\text{[math]}$ ，某渔船在海中的 $\text{[math]}$ 处测得小岛D位于东北方向上，且相距 $\text{[math]}$ ，该渔船自西向东航行一段时间到达点 $\text{[math]}$ 处，此时测得小岛 $\text{[math]}$ 恰好在点 $\text{[math]}$ 的正北方向上，且相距 $\text{[math]}$ ，又测得点 $\text{[math]}$ 与小岛 $\text{[math]}$ 相距 $\text{[math]}$ ．

（1）求 $\text{[math]}$ 的值；

（2）求小岛 $\text{[math]}$ ， $\text{[math]}$ 之间的距离(计算过程中的数据不取近似值)．

查看解析收藏纠错

+选题
9. 如图，某海监船以60海里/时的速度从A处出发沿正西方向巡逻，一可疑船只在A的西北方向的C处，海监船航行1.5小时到达B处时接到报警，需巡査此可疑船只，此时可疑船只仍在B的北偏西 $\text{[math]}$ 方向的C处，然后，可疑船只以一定速度向正西方向逃离，海监船立刻加速以90海里/时的速度追击，在D处海监船追到可疑船只，D在B的北偏西 $\text{[math]}$ 方同．（以下结果保留根号）

（1）求B ， C两处之间的距离；

（2）求海监船追到可疑船只所用的时间．

查看解析收藏纠错

+选题
10. 某地的一座人行天桥如图所示，天桥高为6米，坡面 $\text{[math]}$ 的坡度为 $\text{[math]}$ ，文化墙 $\text{[math]}$ 在天桥底部正前方8米处( $\text{[math]}$ 的长)，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为 $\text{[math]}$ .(参考数据： $\text{[math]}$ ， $\text{[math]}$ )

（1）若新坡面坡角为 $\text{[math]}$ ，求坡角 $\text{[math]}$ 度数；

（2）有关部门规定，文化墙距天桥底部小于3米时应拆除，天桥改造后，该文化墙 $\text{[math]}$ 是否需要拆除？请说明理由.

查看解析收藏纠错

+选题
11. 如图，在Rt△ABC中，∠C＝90°，D为BC上一点，AB＝5，BD＝1，tanB＝ $\text{[math]}$ .

（1）求AD的长；

（2）求sinα的值.

查看解析收藏纠错

+选题
12. 如图是某区域的平面示意图，码头A在观测站B的正东方向，码头A的北偏西 $\text{[math]}$ 方向上有一小岛C，小岛C在观测站B的北偏西 $\text{[math]}$ 方向上，码头A到小岛C的距离AC为10海里.

（1）填空： $\text{[math]}$ 度， $\text{[math]}$ 度；

（2）求观测站B到AC的距离BP（结果保留根号）.

查看解析收藏纠错

+选题
13. 宿迁市政府为了方便市民绿色出行，推出了共享单车服务.图①是某品牌共享单车放在水平地面上的实物图，图②是其示意图，其中 $\text{[math]}$ 、 $\text{[math]}$ 都与地面l平行，车轮半径为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，坐垫 $\text{[math]}$ 与点 $\text{[math]}$ 的距离 $\text{[math]}$ 为 $\text{[math]}$ .

（1）求坐垫 $\text{[math]}$ 到地面的距离；

（2）根据经验，当坐垫 $\text{[math]}$ 到 $\text{[math]}$ 的距离调整为人体腿长的0.8时，坐骑比较舒适.小明的腿长约为 $\text{[math]}$ ，现将坐垫 $\text{[math]}$ 调整至坐骑舒适高度位置 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
（结果精确到 $\text{[math]}$ ，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
14. 如图，海上观察哨所B位于观察哨所A正北方向，距离为25海里.在某时刻，哨所A与哨所B同时发现一走私船，其位置C位于哨所A北偏东53°的方向上，位于哨所B南偏东37°的方向上.
（参考数据：sin37°＝cos53°≈，cos37 ＝sin53°≈去，tan37°≈2，tan76°≈）

（1）求观察哨所A与走私船所在的位置C的距离；

（2）若观察哨所A发现走私船从C处以16海里/小时的速度向正东方向逃窜，并立即派缉私艇沿北偏东76°的方向前去拦截.求缉私艇的速度为多少时，恰好在D处成功拦截.（结果保留根号）

查看解析收藏纠错

+选题
15. 为积极参与鄂州市全国文明城市创建活动，我市某校在教学楼顶部新建了一块大型宣传牌，如下图.小明同学为测量宣传牌的高度AB，他站在距离教学楼底部E处6米远的地面C处，测得宣传牌的底部B的仰角为60°，同时测得教学楼窗户D处的仰角为30°（A、B、D、E在同一直线上）.然后，小明沿坡度i=1：1.5的斜坡从C走到F处，此时DF正好与地面CE平行.

（1）求点F到直线CE的距离(结果保留根号)；

（2）若小明在F处又测得宣传牌顶部A的仰角为45°，求宣传牌的高度AB（结果精确到0.1米， $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73）.

查看解析收藏纠错

+选题
16. 某挖掘机的底座高 $\text{[math]}$ 米，动臂 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 与 $\text{[math]}$ 的固定夹角∠ $\text{[math]}$ =140°．初始位置如图1，斗杆顶点 $\text{[math]}$ 与铲斗顶点 $\text{[math]}$ 所在直线 $\text{[math]}$ 垂直地面 $\text{[math]}$ 于点 $\text{[math]}$ ，测得∠ $\text{[math]}$ =70°(示意图2)．工作时如图3，动臂 $\text{[math]}$ 会绕点 $\text{[math]}$ 转动，当点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一直线时，斗杆顶点 $\text{[math]}$ 升至最高点(示意图4)．

（考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

（1）求挖掘机在初始位置时动臂 $\text{[math]}$ 与 $\text{[math]}$ 的夹角∠ $\text{[math]}$ 的度数．

（2）问斗杆顶点 $\text{[math]}$ 的最高点比初始位置高了多少米(精确到0.1米)?

查看解析收藏纠错

+选题
17. 如图1，已知在平面直角坐标系xOy中，四边形OABC是矩形点A，C分别在x轴和y轴的正半轴上，连结AC，OA＝3，tan∠OAC＝ $\text{[math]}$ ，D是BC的中点.

（1）求OC的长和点D的坐标；

（2）如图2，M是线段OC上的点，OM＝ $\text{[math]}$ OC，点P是线段OM上的一个动点，经过P，D，B三点的抛物线交x轴的正半轴于点E，连结DE交AB于点F
①将△DBF沿DE所在的直线翻折，若点B恰好落在AC上，求此时BF的长和点E的坐标；

②以线段DF为边，在DF所在直线的右上方作等边△DFG，当动点P从点O运动到点M时，点G也随之运动，请直接写出点G运动路径的长.

查看解析收藏纠错

+选题
18. 一名徒步爱好者来衡阳旅行，他从宾馆C出发，沿北偏东30°的方向行走2000米到达石鼓书院A处，参观后又从A处沿正南方向行走一段距离，到达位于宾馆南偏东45°方向的雁峰公园B处，如图所示．

（1）求这名徒步爱好者从石鼓书院走到雁峰公园的途中与宾馆之间的最短距离；

（2）若这名徒步爱好者以100米/分的速度从雁峰公园返回宾馆，那么他在15分钟内能否到达宾馆？

查看解析收藏纠错

+选题
19. 如图所示，山坡上有一棵与水平面垂直的大树，一场台风过后，大树被刮倾斜后折断倒在山坡上，树的顶部恰好接触到坡面．已知山坡的坡角∠AEF=23°，量得树干倾斜角∠BAC=38°，大树被折断部分和坡面所成的角∠ADC=60°，AD=4m．

（1）求∠CAE的度数；

（2）求这棵大树折断前的高度？
（结果精确到个位，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）．

查看解析收藏纠错

+选题
20. 小明、小华在一栋电梯楼前感慨楼房真高．小明说：“这楼起码20层！”小华却不以为然：“20层？我看没有，数数就知道了！”小明说：“有本事，你不用数也能明白！”小华想了想说：“没问题！让我们来量一量吧！”小明、小华在楼体两侧各选A、B两点，测量数据如图，其中矩形CDEF表示楼体，AB=150米，CD=10米，∠A=30°，∠B=45°，（A、C、D、B四点在同一直线上）问：

（1）楼高多少米？

（2）若每层楼按3米计算，你支持小明还是小华的观点呢？请说明理由．（参考数据： $\text{[math]}$ ≈1.73， $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈2.24）

查看解析收藏纠错

+选题
21. 如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．

（1）求灯杆CD的高度；

（2）求AB的长度（结果精确到0.1米）．（参考数据： $\text{[math]}$ =1.73．sin37°≈060，cos37°≈0.80，tan37°≈0.75）

查看解析收藏纠错

+选题
22. 数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α的代数式表示旗杆AB的高度．
数学活动方案
活动时间：2018年4月2日活动地点：学校操场填表人：林平
课题
测量学校旗杆的高度
活动目的
运用所学数学知识及方法解决实际问题
方案示意图
测量步骤
⑴用测得∠ADE=α；
⑵用测得BC=a米，CD=b米．
⑶计算过程

查看解析收藏纠错

+选题
23. 如图，某数学兴趣小组为测量一棵古树BH和教学楼CG的高，先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°，此时教学楼顶端G恰好在视线DH上，再向前走7米到达B处，又测得教学楼顶端G的仰角∠GEF为60°，点A、B、C三点在同一水平线上．

（1）计算古树 BH的高；

（2）计算教学楼CG的高．（参考数据： $\text{[math]}$ ≈14， $\text{[math]}$ ≈1.7）

查看解析收藏纠错

+选题
24. 两栋居民楼之间的距离CD=30米，楼AC和BD均为10层，每层楼高3米．

（1）上午某时刻，太阳光线GB与水平面的夹角为30°，此刻B楼的影子落在A楼的第几层？

（2）当太阳光线与水平面的夹角为多少度时，B楼的影子刚好落在A楼的底部．

查看解析收藏纠错

+选题
25. 如图是小红在一次放风筝活动中某时段的示意图，她在A处时的风筝线（整个过程中风筝线近似地看作直线）与水平线构成30°角，线段AA₁表示小红身高1.5米．

（1）当风筝的水平距离AC=18米时，求此时风筝线AD的长度；

（2）当她从点A跑动9 $\text{[math]}$ 米到达点B处时，风筝线与水平线构成45°角，此时风筝到达点E处，风筝的水平移动距离CF=10 $\text{[math]}$ 米，这一过程中风筝线的长度保持不变，求风筝原来的高度C₁D．

查看解析收藏纠错

+选题
26. 如图，吊车在水平地面上吊起货物时，吊绳BC与地面保持垂直，吊臂AB与水平线的夹角为64°，吊臂底部A距地面1.5m．（计算结果精确到0.1m，参考数据sin64°≈0.90，cos64°≈0.44，tan64°≈2.05）

（1）当吊臂底部A与货物的水平距离AC为5m时，吊臂AB的长为m．

（2）如果该吊车吊臂的最大长度AD为20m，那么从地面上吊起货物的最大高度是多少？（吊钩的长度与货物的高度忽略不计）

查看解析收藏纠错

+选题
27. 下图为某区域部分交通线路图，其中直线 $\text{[math]}$ ，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 都垂直，垂足分别为点A、点B和点C，（高速路右侧边缘）， $\text{[math]}$ 上的点M位于点A的北偏东30°方向上，且BM＝ $\text{[math]}$ 千米， $\text{[math]}$ 上的点N位于点M的北偏东 $\text{[math]}$ 方向上，且 $\text{[math]}$ ，MN= $\text{[math]}$ 千米，点A和点N是城际线L上的两个相邻的站点.

（1）求 $\text{[math]}$ 之间的距离

（2）若城际火车平均时速为150千米/小时，求市民小强乘坐城际火车从站点A到站点N需要多少小时？（结果用分数表示）

查看解析收藏纠错

+选题
28. 如图，在大楼AB正前方有一斜坡CD，坡角∠DCE=30°，楼高AB=60米，在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的D处测得楼顶B的仰角为45°，其中点A，C，E在同一直线上.

（1）求坡底C点到大楼距离AC的值；

（2）求斜坡CD的长度.

查看解析收藏纠错

+选题
29. 如图1，水坝的横截面是梯形ABCD，∠ABC＝37°，坝顶DC＝3m，背水坡AD的坡度i（即tan∠DAB）为1：0.5，坝底AB＝14m．

（1）求坝高；

（2）如图2，为了提高堤坝的防洪抗洪能力，防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固，使得AE＝2DF，EF⊥BF，求DF的长．（参考数据：sin37°≈ $\text{[math]}$ ，cos37°≈ $\text{[math]}$ ，tan37°≈ $\text{[math]}$ ）

查看解析收藏纠错

+选题
30. 知识改变世界，科技改变生活。导航装备的不断更新极大方便了人们的出行.如图，某校组织学生乘车到黑龙滩（用C表示）开展社会实践活动，车到达A地后，发现C地恰好在A地的正北方向，且距离A地13千米，导航显示车辆应沿北偏东60°方向行驶至B地，再沿北偏西37°方向行驶一段距离才能到达C地，求B、C两地的距离.（参考数据：sin53°≈ $\text{[math]}$ ，cos53°≈ $\text{[math]}$ ，tan53°≈ $\text{[math]}$ )

查看解析收藏纠错

+选题

课题	测量学校旗杆的高度
活动目的	运用所学数学知识及方法解决实际问题
方案示意图		测量步骤	⑴用测得∠ADE=α； ⑵用测得BC=a米，CD=b米．
⑶计算过程

解直角三角形的应用专题训练

一、综合题

相关试卷 收起∨

相关试卷收起∨