修改时间:2024-07-13 浏览次数:229 类型:期末考试
|
分数段 |
频数 |
频率 |
|
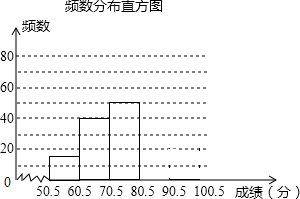
50.5~60.5 |
16 |
0.08 |
|
60.5~70.5 |
40 |
0.2 |
|
70.5~80.5 |
50 |
0.25 |
|
80.5~90.5 |
m |
0.35 |
|
90.5~100.5 |
24 |
n |
试题篮