修改时间:2024-07-13 浏览次数:391 类型:期末考试
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,求证:EF=BE+DF.
解题分析:由于AB=AD,我们可以延长CD到点G,使DG=BE,易得∠ABE=∠ADG=90°,可证△ABE≌△ADG
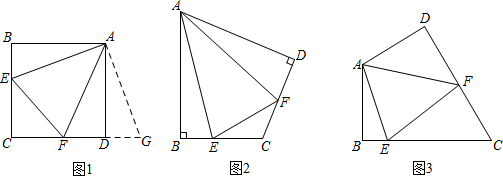
再证明△AFG≌△AFE,得EF=FG=DG+FD=BE+DF
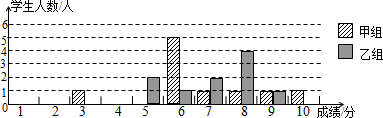
|
组别 |
平均分 |
中位数 |
方差 |
合格率 |
优秀率 |
|
甲 |
6.7 |
|
3.41 |
90% |
20% |
|
乙 |
|
7.5 |
|
80% |
10% |
试题篮