吉林省长春市2020年中考数学二模考试试卷

1. -2020的绝对值是（）

A . -2020 B . $\text{[math]}$ C . $\text{[math]}$ D . 2020

查看解析收藏纠错

+选题
2. 华为Mate20手机搭载了全球首款7纳米制程芯片，7纳米就是0.000 000 007米，数据0.000 000 007用科学记数法表示为（）

A . 7×10^-7 B . 0.7×10^-8 C . 0.7×10^-7 D . 7×10^-9

查看解析收藏纠错

+选题
3. 窗棂是中国传统木构建筑的框架结构设计，窗棂上雕刻有线槽和各种花纹，构成种类繁多的优美图案。下列表示我国古代窗棂样式结构的图案中，既是轴对称，又是中心对称的图形是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 计算(x²y)³的结果是（）

A . x⁶y³ B . x⁵y² C . x⁵y D . x²y³

查看解析收藏纠错

+选题
5. 若使 $\text{[math]}$ 有意义，由x的取值范围是（ )

A . x>3 B . x>-3 C . x≥3． D . x≥-3

查看解析收藏纠错

+选题
6. 在数学活动也就是说上，九年级（1）班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的主亭子B之间的距离，现测得亭子A位于点P北偏西30°方向，亭子B位于点P北偏东a方向，测得点P与亭子A之间的距离为200米，则亭子A与亭子B之间的距离为（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

查看解析收藏纠错

+选题
7. 如图，用三角板作△ABC的边AB上的高，下列三角板的摆放位置正确的是（）

A . B . C . D .

查看解析收藏纠错

+选题
8. 如图，在平面直角坐标系中，Rt△ABC的顶点A，B分别在y轴、x轴上，OA=2，OB=1，斜边AC∥x轴，若反比例函数y= $\text{[math]}$ (k>0，x>0)的图象经过AC的中点D，则k的值为（）

A . 4 B . 5 C . 6 D . 8

查看解析收藏纠错

+选题

9. 因式分解：a³-16a=。

查看解析收藏纠错

+选题
10. 不等式组 $\text{[math]}$ 的解集是。

查看解析收藏纠错

+选题
11. 用举反例的方法，说明命题“关于x的方程x²-4x+m=0一定有实数根”是假命题，则m的值可以是。

查看解析收藏纠错

+选题
12. 《九章算术》是我国古代数学的扛鼎之作，其中记载了这样一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，铭道长一尺，问径几何？”。其大意为：如图AB为圆O的直径，弦CD⊥AB于点E，AE=1寸，CD=10寸，则直径AB的长为寸。

查看解析收藏纠错

+选题
13. 把正五边形和正六边形按如图所示方式放置，则∠a=。

查看解析收藏纠错

+选题
14. 跳台滑雪是冬季奥运会比赛项目之一，运动员起跳后的飞行路线可以看作是抛物线的一部分，运动员起跳后的竖直高度y(单位；米)与水平距离a(单位：米)近似满足函数关系y=ax²+bx+c(a≠0) 。右图记录了某运动员起跳后的x与y的三组数据，根据上述函数模型和数据，可推断出该运动员起跳后飞行到最高点时，水平距离为米。

查看解析收藏纠错

+选题

15. 计算：
$\text{[math]}$

查看解析收藏纠错

+选题
16. 甲、乙两人做摸球游戏，在不透明的口袋里放人大小相同的两个黑球和两个白球，甲摸出两个球后放回并搅匀，乙再摸出两个球，若摸出一黑一白甲赢，若摸出两个相同颜色的乙赢．这个游戏公平吗？为什么？

查看解析收藏纠错

+选题
17. 在大城市，很多上班族选择“低碳出行”、电动车和共享单车成为他们的代步工具。某人去距离家8千米的单位上班，骑共享单车虽然比骑电动车多用20分钟，但却能强身健体．已知他骑电动车的速度是骑共享单车的1.5倍，求他骑共享单车从家到单位上班花费的时间。

查看解析收藏纠错

+选题

18. 中国古代有二十四节气歌：“春雨惊春清谷天，夏满芒夏暑相连，秋处露秋寒霜降，冬雪雪冬小大寒“它是为便于记忆我国古时历法中二十四节气而编成的小诗歌。流传至今，其中第一个”冬“是指立冬，为冬季的开始，但在气象学上的入冬日有是严格定义的，即日平均气温连续五天低于10℃，才算是进入冬天，其中5天中的第一天即为入冬日。

日平均气温是指一天24小时的平均值，气象上通常用一天中的2时、8时、14时、20时4个时刻的气温的平均值作为这一天的日平均气温（即4个气温相加除以4），结果保留一位小数。

下表是长春市某年10月6日至10月12日的气温纪录及日平均气温（单位：℃）

时间	2时	8时	14时	20时	平均气温
10月6日	2	8	18	13	10.3
10月7日	2	7	15	10	a
10月8日	2	7	14	9	8.0
10月9日	2	6	13	9	7.5
10月10日	3	5	9	6	5.8
10月11日	2	5	13	9	7.3
10月12日	4	8	17	13	10.5

根据以上材料解答下列问题：

（1）求出10月7日的日平均气温a；

（2）采用适当的统计图将这7天的日平均气温的变化情况表示出来；

（3）请指出这一年的哪一天是长春市在气象学意义上的入冬日。

查看解析收藏纠错

+选题

19. 如图，△ABC是⊙O的内接三角形，∠ACB=45°，∠AOC=150°，过点C作⊙O的切线交AB的延长线于点D。

（1）求证：CD=CB。

（2）如果⊙O的半径为2，求AC的长。

查看解析收藏纠错

+选题
20. 定义：我们把三边比为1： $\text{[math]}$ ： $\text{[math]}$ 的三角称为尾翼三角形。

（1）请你在下面5×5和2×7的网格中分别画出面积最大的格点尾翼三角形。

（2）尾翼三角形的最大角为度。

查看解析收藏纠错

+选题
21. 周末，甲、乙两名大学生骑自行车去距学校6000米的净月潭公园.两人同时从学校出发，以a米/分的速度匀速行驶.出发4.5分钟时，甲同学发现忘记带学生证，以1.5a米/分的速度按原路返回学校，取完学生证（在学校取学生证所用时间忽略不计），继续以返回时的速度追赶乙.甲追上乙后，两人以相同的速度前往净月潭.乙骑自行车的速度始终不变.设甲、乙两名大学生距学校的路程为s（米），乙同学行驶的时间为t（分），s与t之间的函数图象如图所示.

（1）求a、b的值.

（2）求甲追上乙时，距学校的路程.

（3）当两人相距500米时，直接写出t的值是.

查看解析收藏纠错

+选题
22. 阅读下列材料，完成相应的任务。
数学活动课上，老师提出如下问题：

如图①，在四边形ABCD中，AB⊥BC，DC⊥BC，AB=2，DC=4，BC=8，点P为BC边上的动点，求当BP的值是多少时，AP+DP有最小值，最小值是多少。

小丽和小明对老师提出的问题进行了合作探究：

小丽：设BP=x，则CP=8-x，

根据勾股定理，可得AP+DP= $\text{[math]}$

但没有办法继续求解。

小明：利用轴对称作图，如图②，

作点A关于直线BC的对称点A'，连接A'D，与BC交于点P，

根据两点之间线段最短，将求AP+DP的最小值转化为求线段AD的长。

由△A‘BP∽△DCP，得 $\text{[math]}$

所以BP= $\text{[math]}$

过点A'作A'H⊥DC，交DC的延长线于点H，

再由勾股定理，可得A'D= $\text{[math]}$ =10。

所以当BP= $\text{[math]}$ 时，AP+DP有最小值，最小值为10。

图③

任务：

（1）类比探究：
对于函数y= $\text{[math]}$ ，当x=时，y有最小值，最小值为。

（2）应用拓展：如图③，若点D在BC上运动，AD上BC，AD=3，BC=5。连接AB，AC，求△ABC周长的最小值。

查看解析收藏纠错

+选题
23. 综合与实践

（1）【动手操作】任意一个四边形ABCD通过剪裁，都可以拼接成一个三角形，方法如下：
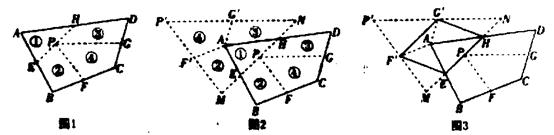
如图1．点E、F、G、H分别是边AB、BC、CD、DA的中点．连结EH，点P是线段EH的中点，连结PF、PG．沿线段EH、PF，PG剪开，将四边形ABCD分成①、②、③、④四部分，按如图所示的方式即可拼成一个无缝隙也不重叠的三角形P'MN。

在拼接过程中用到的图形的变换有。

A．轴对称 B．平移 C．中心对称 D．位似

（2）【性质探究】如图3，连结EF'、F'G'、G'H，判断四边形EF'G'H的形状，并说明理由。

（3）【综合运用】若三角形P'MN是一个边长为4的正三角形，则四边形ABCD周长的最小值为。

查看解析收藏纠错

+选题
24. 如图①，在平面直角坐标系中，当线段AB与坐标轴不垂直时，以线段AB为斜边作Rt△ABC，且边BC⊥x轴，则称AC+BC的值为线段AB的直角距离，记作L(AB)；当线段AB与坐标轴垂直时，线段AB的直角距离不存在。

（1）在平面直角坐标系中，A(1，4)，B(4，2)，求L(AB)。

（2）在平面直角坐标系中．点A与坐标原点重合．点B(x，y)，且L(AB)=2。
①当点B(x：y)在第一象限时，易知AC=x，BC=y，由AC+BC=L(AB)，可得y与x之间的函数关系式为，其中x的取值范围是。

（3）在图②中画出这个函数的图象。
②请模仿①的思考过程，分别探究点B在其它象限的情形，仍然在图②中分别画出点B在二、三、四象限时，y与x的函数图象。(不要求写出探究过程)

（4）在平面直角坐标系中，点A(1，1），点B在抛物线y=a(x-h)²+5上，且2≤L(AB)≤4。
①a= $\text{[math]}$ 时，直接写出h的取值范围。

②当h=0，且△ABC是等腰直角三角形时，直接写出a的取值范围。

查看解析收藏纠错

+选题

吉林省长春市2020年中考数学二模考试试卷

一、选择题（本大题共8小题，每小题3分，共24分）

二、填空题(本大题共6小题，每小题3分，共18分)

三、解答题(本大题共10小题，共78分)

相关试卷收起∨

吉林省长春市2020年中考数学二模考试试卷

一、选择题（本大题共8小题，每小题3分，共24分）

二、填空题(本大题共6小题，每小题3分，共18分)

三、解答题(本大题共10小题，共78分)

相关试卷 收起∨

相关试卷收起∨