贵州省遵义市道真县隆兴中学2019年数学中考二模试卷

修改时间：2024-07-31 浏览次数：291 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 下列说法正确的是（）

A . 负数没有倒数 B . ﹣1的倒数是﹣1 C . 任何有理数都有倒数 D . 正数的倒数比自身小

查看解析收藏纠错

+选题
2. 下列图形中，既是轴对称图形又是中心对称图形的是 $\text{[math]}$ $\text{[math]}$

A . B . C . D .

查看解析收藏纠错

+选题
3. 下列运算正确的是（）

A . a+a＝a² B . a³÷a＝a³ C . a²•a＝a³ D . (a²)³＝a⁵

查看解析收藏纠错

+选题
4. 如图，直线a∥b，直角三角形如图放置，∠DCB=90°，若∠1+∠B=65°，则∠2的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 已知点P（a，3+a）在第二象限，则a的取值范围是（）

A . a＜0 B . a＞﹣3 C . ﹣3＜a＜0 D . a＜﹣3

查看解析收藏纠错

+选题
6. 如图，八个大小相同的小矩形可拼成下面两个大矩形，拼成图2时，中间留下了一个边长为1的小正方形，则每个小矩形的面积是（）

A . 12 B . 14 C . 15 D . 16

查看解析收藏纠错

+选题
7. 某中学篮球队12名队员的年龄情况如下表：
年龄/岁
12
13
14
15
16
人数
1
3
4
2
2
关于这12名队员的年龄，下列说法中正确的是（）

A . 众数为14 B . 极差为3 C . 中位数为13 D . 平均数为14

查看解析收藏纠错

+选题
8. 在关于x的函数 $\text{[math]}$ 中，自变量x的取值范围是（）

A . x≥﹣2 B . x≥﹣2且x≠0 C . x≥﹣2且x≠1 D . x≥1

查看解析收藏纠错

+选题
9. 如图，正方形ABCD的边长为4，动点M、N同时从A点出发，点M沿AB以每秒1个单位长度的速度向中点B运动，点N沿折现ADC以每秒2个单位长度的速度向终点C运动，设运动时间为t秒，则△CMN的面积为S关于t函数的图象大致是（）

A . B . C . D .

查看解析收藏纠错

+选题
10. 下列说法错误的是（）

A . 两组对边分别平行的四边形是平行四边形 B . 两组对边分别相等的四边形是平行四边形 C . 一组对边平行，另一组对边相等的四边形是平行四边形 D . 一组对边平行且相等的四边形是平行四边形

查看解析收藏纠错

+选题
11. 我们可以只用直尺和圆规作出圆的部分内接正多边形.在我们目前所学知识的范围内，下列圆的内接正多边形不可以用尺规作图作出的是（）

A . 正三角形 B . 正四边形 C . 正六边形 D . 正七边形

查看解析收藏纠错

+选题
12. 如图①，分别沿长方形纸片ABCD和正方形纸片EFGH的对角线BD，FH剪开，拼成如图②所示的四边形KLMN，若中间空白部分四边形OPQR恰好是正方形，且四边形KLMN的面积为52，则正方形EFGH的面积是（　　）

A . 24 B . 25 C . 26 D . 27

查看解析收藏纠错

+选题

二、填空题

13. 袋中装有6个黑球和n个白球，经过若干次试验，发现“若从袋中任摸出一个球，恰是黑球的概率为 $\text{[math]}$ ，则这个袋中白球大约有个．

查看解析收藏纠错

+选题
14. (x-3y)(x+3y)=.

查看解析收藏纠错

+选题
15. 如图，AB是半圆O的直径，点C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点P，连接AC，BC， $\text{[math]}$ ，AD=3.给出下列结论：①AC平分∠BAD；②△ABC∽△ACE；③AB=3PB；④S_△_ABC=5，其中正确的是（写出所有正确结论的序号）.

查看解析收藏纠错

+选题
16. 如图，在平面直角坐标系中，矩形ABCD的边AB：BC=3：2，点A（-3，0），B（0，6）分别在x轴，y轴上，反比例函数y= $\text{[math]}$ （x＞0）的图象经过点D，且与边BC交于点E，则点E的坐标为.

查看解析收藏纠错

+选题

三、解答题

17. 计算： $\text{[math]}$

查看解析收藏纠错

+选题
18. 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

查看解析收藏纠错

+选题
19. 黄岩岛自古以来就是中国的领土，如图，为维护海洋利益，三沙市一艘海监船在黄岩岛附近海域巡航，某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向，海监船沿北偏西30°方向航行60海里后到达B处，此时测得该目标C在它的南偏东75方向，求此时该船与目标C之间的距离CB的长度，（结果保留根号）

查看解析收藏纠错

+选题

20. 现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）：

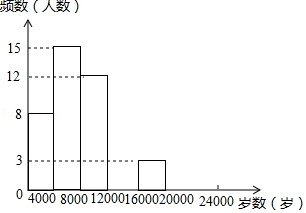
步数	频数	频率
0≤x＜4000	8	a
4000≤x＜8000	15	0.3
8000≤x＜12000	12	b
12000≤x＜16000	c	0.2
16000≤x＜20000	3	0.06
20000≤x＜24000	d	0.04

请根据以上信息，解答下列问题：

（1）写出a，b，c，d的值并补全频数分布直方图；

（2）本市约有37800名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？

（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步的两名教师与大家分享心得，求被选取的两名教师恰好都在20000步（包含20000步）以上的概率.

查看解析收藏纠错

+选题

21. 如图，在平面直角坐标系中，以坐标原点O为圆心，2为半径画圆，P是⊙O上一动点且在第一象限内，过点P作⊙O的切线，与x、y轴分别交于点A、B.

（1）求证：△OBP与△OPA相似；

（2）当点P为AB中点时，求出P点坐标；

（3）在⊙O上是否存在一点Q，使得以Q，O，A、P为顶点的四边形是平行四边形.若存在，试求出Q点坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题
22. 某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．

（1）求每台A型电脑和B型电脑的销售利润；

（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？

查看解析收藏纠错

+选题
23. 如图，已知直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 相交于A，B两点，且点A（1，－4）为抛物线的顶点，点B在x轴上。

（1）求抛物线的解析式；

（2）在（1）中抛物线的第二象限图象上是否存在一点P，使△POB与△POC全等？若存在，求出点P的坐标；若不存在，请说明理由；

（3）若点Q是y轴上一点，且△ABQ为直角三角形，求点Q的坐标。

查看解析收藏纠错

+选题
24. 如图1，在平面直角坐标系中，一次函数y＝﹣2x+8的图象与x轴，y轴分别交于点A，点C，过点A作AB⊥x轴，垂足为点A，过点C作CB⊥y轴，垂足为点C，两条垂线相交于点B.

（1）线段AB，BC，AC的长分别为AB＝，BC＝，AC＝；

（2）折叠图1中的△ABC，使点A与点C重合，再将折叠后的图形展开，折痕DE交AB于点D，交AC于点E，连接CD，如图2.
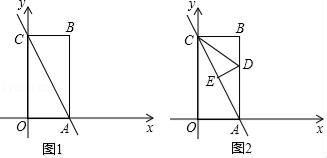
请从下列A、B两题中任选一题作答，我选择（）题.

A：①求线段AD的长；

②在y轴上，是否存在点P，使得△APD为等腰三角形？若存在，请直接写出符合条件的所有点P的坐标；若不存在，请说明理由.

B：①求线段DE的长；

②在坐标平面内，是否存在点P（除点B外），使得以点A，P，C为顶点的三角形与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题

年龄/岁	12	13	14	15	16
人数	1	3	4	2	2

贵州省遵义市道真县隆兴中学2019年数学中考二模试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨