2017年江苏省扬州市中考数学试卷

1. 若数轴上表示﹣1和3的两点分别是点A和点B，则点A和点B之间的距离是（）

A . ﹣4 B . ﹣2 C . 2 D . 4

查看解析收藏纠错

+选题
2. 下列算式的运算结果为a⁴的是（）

A . a⁴•a B . （a²）² C . a³+a³ D . a⁴÷a

查看解析收藏纠错

+选题
3. 一元二次方程x²﹣7x﹣2=0的实数根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 不能确定

查看解析收藏纠错

+选题
4. 下列统计量中，反映一组数据波动情况的是（）

A . 平均数 B . 众数 C . 频率 D . 方差

查看解析收藏纠错

+选题
5. 经过圆锥顶点的截面的形状可能是（）

A . B . C . D .

查看解析收藏纠错

+选题
6. 若一个三角形的两边长分别为2和4，则该三角形的周长可能是（）

A . 6 B . 7 C . 11 D . 12

查看解析收藏纠错

+选题
7. 在一列数：a₁ ， a₂ ， a₃ ， …，a_n中，a₁=3，a₂=7，从第三个数开始，每一个数都等于它前两个数之积的个位数字，则这一列数中的第2017个数是（）

A . 1 B . 3 C . 7 D . 9

查看解析收藏纠错

+选题
8. 如图，已知△ABC的顶点坐标分别为A（0，2）、B（1，0）、C（2，1），若二次函数y=x²+bx+1的图象与阴影部分（含边界）一定有公共点，则实数b的取值范围是（）

A . b≤﹣2 B . b＜﹣2 C . b≥﹣2 D . b＞﹣2

查看解析收藏纠错

+选题

9. 2017年5月18日，我国在南海北部神弧海域进行的可燃冰试开采成功，标志着我国成为全球第一个在海域可燃冰开采中获得连续稳定的国家．目前每日的天然气试开采量约为16000立方米，把16000立方米用科学记数法表示为立方米．

查看解析收藏纠错

+选题
10. 若 $\text{[math]}$ =2， $\text{[math]}$ =6，则 $\text{[math]}$ =．

查看解析收藏纠错

+选题
11. 因式分解：3x²﹣27=．

查看解析收藏纠错

+选题
12. 在平行四边形ABCD中，∠B+∠D=200°，则∠A=．

查看解析收藏纠错

+选题
13. 为了了解某班数学成绩情况，抽样调查了13份试卷成绩，结果如下：3个140分，4个135分，2个130分，2个120分，1个100分，1个80分．则这组数据的中位数为分．

查看解析收藏纠错

+选题
14. 同一温度的华氏度数y（℉）与摄氏度数x（℃）之间的函数表达式是y= $\text{[math]}$ x+32．若某一温度的摄氏度数值与华氏度数值恰好相等，则此温度的摄氏度数为℃．

查看解析收藏纠错

+选题
15. 如图，已知⊙O是△ABC的外接圆，连接AO，若∠B=40°，则∠OAC=°．

查看解析收藏纠错

+选题
16. 如图，把等边△A BC沿着D E折叠，使点A恰好落在BC边上的点P处，且DP⊥BC，若BP=4cm，则EC=cm．

查看解析收藏纠错

+选题
17.
如图，已知点A是反比例函数y=﹣ $\text{[math]}$ 的图象上的一个动点，连接OA，若将线段O A绕点O顺时针旋转90°得到线段OB，则点B所在图象的函数表达式为．

查看解析收藏纠错

+选题
18. 若关于x的方程﹣2x+m $\text{[math]}$ +4020=0存在整数解，则正整数m的所有取值的和为．

查看解析收藏纠错

+选题

19. 计算或化简：

（1） ﹣2²+（π﹣2017）⁰﹣2sin60°+|1﹣ $\text{[math]}$ |；

（2） a（3﹣2a）+2（a+1）（a﹣1）．

查看解析收藏纠错

+选题
20. 解不等式组 $\text{[math]}$ ，并求出它的所有整数解．

查看解析收藏纠错

+选题
21. “富春包子”是扬州特色早点，富春茶社为了了解顾客对各种早点的喜爱情况，设计了如右图的调查问卷，对顾客进行了抽样调查．根据统计数据绘制了如下尚不完整的统计图．
根据以上信息，解决下列问题：

（1）条形统计图中“汤包”的人数是，扇形统计图中“蟹黄包”部分的圆心角为°；

（2）根据抽样调查结果，请你估计富春茶社1000名顾客中喜欢“汤包”的有多少人？

查看解析收藏纠错

+选题
22. 车辆经过润扬大桥收费站时，4个收费通道 A、B、C、D中，可随机选择其中的一个通过．

（1）一辆车经过此收费站时，选择 A通道通过的概率是；

（2）求两辆车经过此收费站时，选择不同通道通过的概率．

查看解析收藏纠错

+选题
23. 星期天，小明和小芳从同一小区门口同时出发，沿同一路线去离该小区1800米的少年宫参加活动，为响应“节能环保，绿色出行”的号召，两人都步行，已知小明的速度是小芳的速度的1.2倍，结果小明比小芳早6分钟到达，求小芳的速度．

查看解析收藏纠错

+选题
24.
如图，将△ABC沿着射线BC方向平移至△A'B'C'，使点A'落在∠ACB的外角平分线CD上，连结AA'．

（1）判断四边形ACC'A'的形状，并说明理由；

（2）在△ABC中，∠B=90°，A B=24，cos∠BAC= $\text{[math]}$ ，求CB'的长．

查看解析收藏纠错

+选题
25. 如图，已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上，过点C作CD⊥AB，分别交AB、AO的延长线于点D、E，AE交半圆O于点F，连接CF．

（1）判断直线DE与半圆O的位置关系，并说明理由；

（2） ①求证：CF=OC；
②若半圆O的半径为12，求阴影部分的周长．

查看解析收藏纠错

+选题
26. 我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“极化值”就等于AO²﹣BO²的值，可记为AB△AC=AO²﹣BO² ．

（1）
在图1中，若∠BAC=90°，AB=8，AC=6，AO是BC边上的中线，则AB△AC=，OC△OA=；

（2）
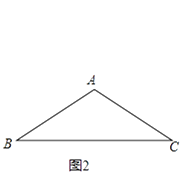
如图2，在△ABC中，AB=AC=4，∠BAC=120°，求AB△AC、BA△BC的值；

（3）
如图3，在△ABC中，AB=AC，AO是BC边上的中线，点N在AO上，且ON= $\text{[math]}$ AO．已知AB△AC=14，BN△BA=10，求△ABC的面积．

查看解析收藏纠错

+选题
27. 农经公司以30元/千克的价格收购一批农产品进行销售，为了得到日销售量p（千克）与销售价格x（元/千克）之间的关系，经过市场调查获得部分数据如下表：
销售价格x（元/千克）
30
35
40
45
50
日销售量p（千克）
600
450
300
150
0

（1）请你根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式；

（2）农经公司应该如何确定这批农产品的销售价格，才能使日销售利润最大？

（3）若农经公司每销售1千克这种农产品需支出a元（a＞0）的相关费用，当40≤x≤45时，农经公司的日获利的最大值为2430元，求a的值．（日获利=日销售利润﹣日支出费用）

查看解析收藏纠错

+选题
28. 如图，已知正方形ABCD的边长为4，点P是AB边上的一个动点，连接CP，过点P作PC的垂线交AD于点E，以 PE为边作正方形PEFG，顶点G在线段PC上，对角线EG、PF相交于点O．

（1）若AP=1，则AE=；

（2） ①求证：点O一定在△APE的外接圆上；
②当点P从点A运动到点B时，点O也随之运动，求点O经过的路径长；

（3）在点P从点A到点B的运动过程中，△APE的外接圆的圆心也随之运动，求该圆心到AB边的距离的最大值．

查看解析收藏纠错

+选题

2017年江苏省扬州市中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷收起∨

销售价格x（元/千克）	30	35	40	45	50
日销售量p（千克）	600	450	300	150	0

2017年江苏省扬州市中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨