2017年广西百色市中考数学试卷

修改时间：2024-07-12 浏览次数：868 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 化简：|﹣15|等于（）

A . 15 B . ﹣15 C . ±15 D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 多边形的外角和等于（）

A . 180° B . 360° C . 720° D . （n﹣2）•180°

查看解析收藏纠错

+选题
3. 在以下一列数3，3，5，6，7，8中，中位数是（）

A . 3 B . 5 C . 5.5 D . 6

查看解析收藏纠错

+选题
4. 下列计算正确的是（）

A . （﹣3x）³=﹣27x³ B . （x^﹣2）²=x⁴ C . x²÷x^﹣2=x² D . x^﹣1•x^﹣2=x²

查看解析收藏纠错

+选题
5.
如图，AM为∠BAC的平分线，下列等式错误的是（）

A . $\text{[math]}$ ∠BAC=∠BAM B . ∠BAM=∠CAM C . ∠BAM=2∠CAM D . 2∠CAM=∠BAC

查看解析收藏纠错

+选题
6. 5月14﹣15日“一带一路”论坛峰会在北京隆重召开，促进了我国与世界各国的互联互通互惠，“一带一路”地区覆盖总人数约为44亿人，44亿这个数用科学记数法表示为（）

A . 4.4×10⁸ B . 4.4×10⁹ C . 4×10⁹ D . 44×10⁸

查看解析收藏纠错

+选题
7.
如图所示的正三棱柱，它的主视图、俯视图、左视图的顺序是（）

A . ①②③ B . ②①③ C . ③①② D . ①③②

查看解析收藏纠错

+选题
8. 观察以下一列数的特点：0，1，﹣4，9，﹣16，25，…，则第11个数是（）

A . ﹣121 B . ﹣100 C . 100 D . 121

查看解析收藏纠错

+选题
9.
九年级（2）班同学根据兴趣分成五个小组，各小组人数分布如图所示，则在扇形图中，第一小组对应的圆心角度数是（）

A . 45° B . 60° C . 72° D . 120°

查看解析收藏纠错

+选题
10.
如图，在距离铁轨200米的B处，观察由南宁开往百色的“和谐号”动车，当动车车头在A处时，恰好位于B处的北偏东60°方向上；10秒钟后，动车车头到达C处，恰好位于B处的西北方向上，则这时段动车的平均速度是（）米/秒．

A . 20（ $\text{[math]}$ +1） B . 20（ $\text{[math]}$ ﹣1） C . 200 D . 300

查看解析收藏纠错

+选题
11. 以坐标原点O为圆心，作半径为2的圆，若直线y=﹣x+b与⊙O相交，则b的取值范围是（）

A . 0≤b＜2 $\text{[math]}$ B . ﹣2 $\text{[math]}$ C . ﹣2 $\text{[math]}$ 2 $\text{[math]}$ D . ﹣2 $\text{[math]}$ ＜b＜2 $\text{[math]}$

查看解析收藏纠错

+选题
12. 关于x的不等式组 $\text{[math]}$ 的解集中至少有5个整数解，则正数a的最小值是（）

A . 3 B . 2 C . 1 D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

13. 若分式 $\text{[math]}$ 有意义，则x的取值范围为．

查看解析收藏纠错

+选题
14. 一个不透明的盒子里有5张完全相同的卡片，它们的标号分别为1，2，3，4，5，随机抽取一张，抽中标号为奇数的卡片的概率是．

查看解析收藏纠错

+选题
15. 下列四个命题中：①对顶角相等；②同旁内角互补；③全等三角形的对应角相等；④两直线平行，同位角相等，其中假命题的有（填序号）

查看解析收藏纠错

+选题
16.
如图，在正方形OABC中，O为坐标原点，点C在y轴正半轴上，点A的坐标为（2，0），将正方形OABC沿着OB方向平移 $\text{[math]}$ OB个单位，则点C的对应点坐标为．

查看解析收藏纠错

+选题
17. 经过A（4，0），B（﹣2，0），C（0，3）三点的抛物线解析式是．

查看解析收藏纠错

+选题
18.
阅读理解：用“十字相乘法”分解因式2x²﹣x﹣3的方法．
（i）二次项系数2=1×2；
（ii）常数项﹣3=﹣1×3=1×（﹣3），验算：“交叉相乘之和”；
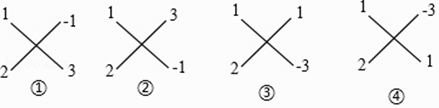
1×3+2×（﹣1）=1 1×（﹣1）+2×3=5 1×（﹣3）+2×1=﹣1 1×1+2×（﹣3）=﹣5
（iii）发现第③个“交叉相乘之和”的结果1×（﹣3）+2×1=﹣1，等于一次项系数﹣1．
即：（x+1）（2x﹣3）=2x²﹣3x+2x﹣3=2x²﹣x﹣3，则2x²﹣x﹣3=（x+1）（2x﹣3）．
像这样，通过十字交叉线帮助，把二次三项式分解因式的方法，叫做十字相乘法．仿照以上方法，分解因式：3x²+5x﹣12=．

查看解析收藏纠错

+选题

三、解答题

19. 计算： $\text{[math]}$ +（ $\text{[math]}$ ）^﹣1﹣（3﹣π）⁰﹣|1﹣4cos30°|

查看解析收藏纠错

+选题
20. 已知a=b+2018，求代数式 $\text{[math]}$ • $\text{[math]}$ ÷ $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
21.
已知反比例函数y= $\text{[math]}$ （k≠0）的图象经过点B（3，2），点B与点C关于原点O对称，BA⊥x轴于点A，CD⊥x轴于点D．

（1）求这个反比函数的解析式；

（2）求△ACD的面积．

查看解析收藏纠错

+选题
22.
矩形ABCD中，E、F分别是AD、BC的中点，CE、AF分别交BD于G、H两点．
求证：

（1）四边形AFCE是平行四边形；

（2）证明：EG=FH．

查看解析收藏纠错

+选题
23.
甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全）：
次数
运动员
1
2
3
4
5
甲
10
8
9
10
8
乙
10
9
9
a
b
某同学计算出了甲的成绩平均数是9，方差是
S_甲²= $\text{[math]}$ [（10﹣9）²+（8﹣9）²+（9﹣9）²+（10﹣9）²+（8﹣9）²]=0.8，请作答：

（1）在图中用折线统计图将甲运动员的成绩表示出来；

（2）若甲、乙射击成绩平均数都一样，则a+b=；

（3）在（2）的条件下，当甲比乙的成绩较稳定时，请列举出a、b的所有可能取值，并说明理由．

查看解析收藏纠错

+选题
24. 某校九年级10个班级师生举行毕业文艺汇演，每班2个节目，有歌唱与舞蹈两类节目，年级统计后发现唱歌类节目数比舞蹈类节目数的2倍少4个．

（1）九年级师生表演的歌唱与舞蹈类节目数各有多少个？

（2）该校七、八年级师生有小品节目参与，在歌唱、舞蹈、小品三类节目中，每个节目的演出平均用时分别是5分钟、6分钟、8分钟，预计所有演出节目交接用时共花15分钟，若从20：00开始，22：30之前演出结束，问参与的小品类节目最多能有多少个？

查看解析收藏纠错

+选题
25.
已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F，若 $\text{[math]}$ = $\text{[math]}$ ，如图1，．

（1）判断△ABC的形状，并证明你的结论；

（2）
设AE与DF相交于点M，如图2，AF=2FC=4，求AM的长．

查看解析收藏纠错

+选题
26.
以菱形ABCD的对角线交点O为坐标原点，AC所在的直线为x轴，已知A（﹣4，0），B（0，﹣2），M（0，4），P为折线BCD上一动点，作PE⊥y轴于点E，设点P的纵坐标为a．

（1）求BC边所在直线的解析式；

（2）设y=MP²+OP² ，求y关于a的函数关系式；

（3）当△OPM为直角三角形时，求点P的坐标．

查看解析收藏纠错

+选题

2017年广西百色市中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨