2019年浙江省中考数学分类汇编专题12：统计与概率（数据收集、整理与分析）

修改时间：2019-07-11 浏览次数：478 类型：二轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 对温州某社区居民最爱吃的鱼类进行问卷调查后（每人选一种），绘制成如图所示统计图．已知选择鲳鱼的有40人，那么选择黄鱼的有（）

A . 20人 B . 40人 C . 60人 D . 80人

查看解析收藏纠错

+选题
2. 方差是刻画数据波动程度的量，对于一组数据x·x₁·…x_n ，可用如下算式计算方差s²= $\text{[math]}$ [（x₁-5）²+（x₂-5）²+.…+（x_n-5）²]，其中“5”是这组数据的（）

A . 最小值 B . 平均数 C . 中位数 D . 众数

查看解析收藏纠错

+选题
3. 点点同学对数据26，36，36，46，5■，52进行统计分析，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（）

A . 平均数 B . 中位数 C . 方差 D . 标准差

查看解析收藏纠错

+选题
4. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵，每棵产量的平均数x（单位：千克）及方差S²（单位：千克²）如下表所示：

甲

乙

丙

丁

x

24

24

23

20

S²

2.1

1.9

2

1.9

今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题

5. 某地一周前四天每天的最高气温与最低气温如表，则这四天中温差最大的是（）

星期	一	二	三	四
最高气温	10℃	12℃	11℃	9℃
最低气温	3℃	0℃	-2℃	-3℃

A . 星期一 B . 星期二 C . 星期三 D . 星期四

查看解析收藏纠错

+选题

6. $\text{[math]}$ 年 $\text{[math]}$ 月 $\text{[math]}$ 日第 $\text{[math]}$ 届中国国际大数据产业博览会召开．某市在五届数博会上的产业签约金额的折线统计图如图．下列说法正确的是（）

A . 签约金额逐年增加 B . 与上年相比，2019年的签约金额的增长量最多 C . 签约金额的年增长速度最快的是2016年 D . 2018年的签约金额比2017年降低了22.98%

查看解析收藏纠错

+选题

二、填空题

7. 数据2，7，5，7，9的众数是。

查看解析收藏纠错

+选题
8. 数据3，4，10，7，6的中位数是．

查看解析收藏纠错

+选题
9. 某校学生“汉字听写”大赛成绩的频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，其中成绩为“优良”（80分及以上）的学生有人．

查看解析收藏纠错

+选题
10. 学校进行广播操比赛，如图是20位评委给某班的评分情况统计图，则该班的平均得分是分.

查看解析收藏纠错

+选题
11. 某计算机程序第一次算得m个数据的平均数为x，第二次算得另外n个数据的平均数为y，则这m+n个数据的平均数等于。

查看解析收藏纠错

+选题

三、综合题

12. 车间有20名工人，某天他们生产的零件个数统计如下表．

车间20名工人某一天生产的零件个数统计表

生产零件的个数（个）	9	10	11	12	13	15	16	19	20
工人人数（人）	1	1	6	4	2	2	2	1	1

（1）求这一天20名工人生产零件的平均个数；

（2）为了提高大多数工人的积极性，管理者准备实行“每天定额生产，超产有奖”的措施．如果你是管理者，从平均数、中位数、众数的角度进行分析，你将如何确定这个“定额”？

查看解析收藏纠错

+选题

13. 在“创全国文明城市”活动中，某社区为了了解居民掌握垃圾分类知识的情况进行调查．其中A、B 两小区分别有 500 名居民参加了测试，社区从中各随机抽取50 名居民成绩进行整理得到部分信息：
【信息一】A 小区 50 名居民成绩的频数直方图如下(每一组含前一个边界值，不含后一个边界值)：

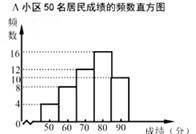
【信息二】上图中，从左往右

第四组的成绩如下

【信息三】A、B 两小区各 50 名居民成绩的平均数、中位数、众数、优秀率(80 分及以上为优秀)、方差等数据如下(部分空缺)：

根据以上信息，回答下列问题：

（1）求A小区50名居民成绩的中位数．

（2）请估计A小区500名居民成绩能超过平均数的人数．

（3）请尽量从多个角度，选择合适的统计量分析 A，B 两小区参加测试的居民掌握垃圾分类知识的情况．

查看解析收藏纠错

+选题
14. 建国七十周年到来之际，海庆中学决定举办以“祖国在我心中”为主题的读书活动．为了使活动更具有针对性，学校在全校范围内随机抽取部分学生进行问卷调查，要求学生在“教育、科技、国防、农业、工业”五类书籍中，选取自己最想读的一种（必选且只选一种）．学校将收集到的调查结果适当整理后，绘制成如图所示的不完整的统计图．请根据图中所给的信息解答下列问题：

（1）在这次调查中，一共抽取了多少名学生?

（2）请通过计算补全条形统计图；

（3）如果海庆中学共有1500名学生，请你估计该校最想读科技类书籍的学生有多少名．

查看解析收藏纠错

+选题
15. 在推进嘉兴市城乡生活垃圾分类的行动中，某社区为了了解居民掌握垃圾分类知识的情况进行调查．其中A、B 两小区分别有 500 名居民参加了测试，社区从中各随机抽取50 名居民成绩进行整理得到部分信息：
【信息一】A 小区 50 名居民成绩的频数直方图如下(每一组含前一个边界值，不含后一个边界值)：

【信息二】上图中，从左往右

第四组的成绩如下

75 75 79 79 79 79 80 80

81 82 82 83 83 84 84 84

【信息三】A、B 两小区各 50 名居民成绩的平均数、中位数、众数、优秀率(80 分及以上为优秀)、方差等数据如下(部分空缺)：

小区平均数中位数众数优秀率方差

A 75.1 △ 79 40% 277

B 75.1 77 76 45% 211

根据以上信息，回答下列问题：

（1）求A小区50名居民成绩的中位数．

（2）请估计A小区500名居民成绩能超过平均数的人数．

（3）请尽量从多个角度，选择合适的统计量分析 A，B 两小区参加测试的居民掌握垃圾分类知识的情况．

查看解析收藏纠错

+选题
16. 小明、小聪参加了100m跑的5期集训，每期集训结束时进行测试，根据他们的集训时间、测试成绩绘制成如下两个统计图。

根据图中信息，解答下列问题：

（1）这5期的集训共有多少天？小聪5次测试的平均成绩是多少?

（2）根据统计数据，结合体育运动的实际，从集训时间和测试成绩这两方面，说说你的想法.。

查看解析收藏纠错

+选题
17. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害，为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动，在活动前和活动后分别随机抽取了部分使用电瓶车的市民，就骑电瓶车安全帽情况进行问卷调查，将收集的数据制成如下统计图表
活动前骑电车戴安全帽情况统计表
类别
人数
A
68
B
245
C
510
D
177
合计
1000
活动后骑电车戴安全帽情况统计图

（1）宣传活动前，在抽取的市民中哪一类别的人数最多？占抽取人数的百分之几？

（2）该市约有30万人使用电瓶车，请估计活动前全市骑电瓶车“都不戴”安全帽的总人数；

（3）小明认为，宣传活动后骑电瓶车“都不敲”安全帽的人数为178，比活动前增加了1人，因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理？请结合统计图表，对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法

查看解析收藏纠错

+选题
18. 我市自开展“学习新思想，做好接班人”主题阅读活动以来，受到各校的广泛关注和同学们的积极响应，某校为了解全校学生主题阅读的情况，随机抽查了部分学生在某一周主题阅读文章的篇数，并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表

文章阅读的篇数(篇)

3

4

5

6

7及以上

人数(人)

20

28

m

16

12

某校抽查的学生文章阅读的篇数情况统计图

请根据统计图表中的信息，解答下列问题：

（1）求被抽查的学生人数和m的值；

（2）求本次抽查的学生文章阅读篇数的中位数和众数；

（3）若该校共有800名学生，根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.

查看解析收藏纠错

+选题
19. 某校为积极响应“南孔圣地，衢州有礼”城市品牌建设，在每周五下午第三节课开展了丰富多彩的走班选课活动。其中综合实践类共开设了“礼行”“礼知”“礼思”“礼艺”“礼源”等五门课程，要求全校学生必须参与其中一门课程。为了解学生参与综合实践类课程活动情况，随机抽取了部分学生进行调查，根据调查结果绘制了如图所示不完整的条形统计图和扇形统计图。

（1）请问被随机抽取的学生共有多少名?并补全条形统计图。

（2）在扇形统计图中，求选择“礼行”课程的学生人数所对应的扇形圆心角的度数。

（3）若该校共有学生1200人，估计其中参与“礼源”课程的学生共有多少人？

查看解析收藏纠错

+选题
20. 称量五筐水果的质量，若每筐以50千克为基准，超过基准部分的千克数记为正数，不足基准部分的千克数记为负数.甲组为实际称量读数，乙组为记录数据。并把所得数据整理成如下统计表和未完成的统计图（单位：千克）.

（1）补充完整乙组数据的折线统计图。

（2） ①甲，乙两组数据的平均数分别为了 $\text{[math]}$ ， $\text{[math]}$ ，写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的等量关系.
②甲，乙两组数据的方差分别为S_甲² ， S_乙² ，比较S_甲²与S_乙²的大小，并说明理由.

查看解析收藏纠错

+选题
21. 今年5月15日，亚洲文明对话大会在北京开幕.为了增进学生对亚洲文化的了解，某学校开展了相关知识的宣传教育活动。为了解这次宣传活动的效果，学校从全校1200名学生中随机抽取100名学生进行知识测试（测试满分100分，得分均为整数），并根据这100人的测试成绩，
制作了如下统计图表。

由图表中给出的信息回答下列问题：

（1） m=，并补全额数直方图；

（2）小明在这次测试中成绩为85分，你认为85分一定是这100名学生知识测试成绩的中位数吗?请简要说明理由；

（3）如果80分以上（包括80分）为优秀，请估计全校1200名学生中成绩优秀的人数.

查看解析收藏纠错

+选题
22. 某校根据课程设置要求，开设了数学类拓展性课程。为了解学生最喜欢的课程内容，随机抽取了部分学生进行问卷调查（生人必须且只选其中一项），并将统计结果绘制成如下统计图（不完整），请根据图中信息回答问题。

（1）求m，n的值。

（2）补全条形统计图。

（3）该校共有1200名学生，试估计全校最喜欢“数学史话”的学生人数。

查看解析收藏纠错

+选题

小区	平均数	中位数	众数	优秀率	方差
A	75.1	△	79	40%	277
B	75.1	77	76	45%	211

文章阅读的篇数(篇)	3	4	5	6	7及以上
人数(人)	20	28	m	16	12

	甲	乙	丙	丁
x	24	24	23	20
S²	2.1	1.9	2	1.9

类别	人数
A	68
B	245
C	510
D	177
合计	1000

2019年浙江省中考数学分类汇编专题12：统计与概率（数据收集、整理与分析）

一、单选题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨