黑龙江省哈尔滨市平房区2019年中考数学二模试卷

1. a，b是有理数，它们在数轴上的对应点的位置如图所示，把a，﹣a，b，﹣b按照从小到大的顺序排列（）

A . ﹣b＜﹣a＜a＜b B . ﹣a＜﹣b＜a＜b C . ﹣b＜a＜﹣a＜b D . ﹣b＜b＜﹣a＜a

查看解析收藏纠错

+选题
2. 下列计算正确的是（）

A . a³+a²＝a⁵ B . a³•a²＝a⁵ C . (2a²)³＝6a⁶ D . a⁶÷a²＝a³

查看解析收藏纠错

+选题
3. 下图中是中心对称图形而不是轴对称图形的共有（）

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
4. 将一个正方体沿图1所示切开，形成如图2的图形，则图2的左视图为（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 已知反比例函数y＝﹣ $\text{[math]}$ ，下列结论中不正确的是（）

A . 图象必经过点（﹣3，2） B . 图象位于第二、四象限 C . 若x＜﹣2，则0＜y＜3 D . 在每一个象限内，y随x值的增大而减小

查看解析收藏纠错

+选题
6. 若不等式组 $\text{[math]}$ 有2个整数解，则a的取值范围为（）

A . ﹣1＜a＜0 B . ﹣1≤a＜0 C . ﹣1＜a≤0 D . ﹣1≤a≤0

查看解析收藏纠错

+选题
7. 如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD＝12 m，塔影长DE＝18 m，小明和小华的身高都是1.6m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，那么塔高AB为（）

A . 24m B . 22m C . 20m D . 18m

查看解析收藏纠错

+选题
8. 如图，将Rt△ABC（∠B＝35°，∠C＝90°）绕点A按顺时针方向旋转到△AB₁C₁的位置，使得点C，A，B₁在同一条直线上，那么旋转角等于（）

A . 55° B . 70° C . 125° D . 145°

查看解析收藏纠错

+选题
9. 如图，在△ABC中，点D、E分别在AB、AC上，DE∥BC，若AD＝2，DB＝1，△ADE、△ABC的面积分别为S₁、S₂ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

查看解析收藏纠错

+选题
10. 在正方形ABCD中，点E为BC边的中点，点F在对角线AC上，连接FB、FE．当点F在AC上运动时，设AF＝x，△BEF的周长为y，下列图象中，能表示y与x的函数关系的图象大致是（）

A . B . C . D .

查看解析收藏纠错

+选题

11. 现在网购越来越多地成为人们的一种消费方式，刚刚过去的2015年的“双11”网上促销活动中，天猫和淘宝的支付交易额突破67000000000元，将67000000000元用科学记数法表示为．

查看解析收藏纠错

+选题
12. 函数y＝ $\text{[math]}$ 中，自变量x的取值范围是．

查看解析收藏纠错

+选题
13. 计算：（ $\text{[math]}$ + $\text{[math]}$ ）﹣ $\text{[math]}$ 的结果是．

查看解析收藏纠错

+选题
14. 分解因式：3x²﹣6x²y+3xy²=．

查看解析收藏纠错

+选题
15. 已知二次函数y＝x²﹣8x+m的最小值为1，那么m的值等于．

查看解析收藏纠错

+选题
16. 已知一个半径为4的扇形的面积为12π，则此扇形的弧长为．

查看解析收藏纠错

+选题
17. 袋中装有一个红球和二个黄球，它们除了颜色外都相同，随机从中摸出一球，记录下颜色后放回袋中，充分摇匀后，再随机摸出一球，两次都摸到红球的概率是．

查看解析收藏纠错

+选题
18. 某工艺品车间有20名工人，平均每人每天可制作12个大花瓶或10个小饰品，已知2个大花瓶与5个小饰品配成一套，则要安排名工人制作大花瓶，才能使每天制作的大花瓶和小饰品刚好配套．

查看解析收藏纠错

+选题
19. 在△ABC中，∠A，∠B都是锐角，且sinA＝ $\text{[math]}$ ，tanB＝ $\text{[math]}$ ，AB＝10，则△ABC的面积为．

查看解析收藏纠错

+选题
20. 如图，△ABC中，点E是BC上的一点，CE＝2BE，点D是AC中点，若S_△ABC＝12，则S_△ADF﹣S_△BEF＝．

查看解析收藏纠错

+选题

21. 先化简再求值： $\text{[math]}$ ÷（a﹣ $\text{[math]}$ ），其中a＝2cos30°+1，b＝tan45°．

查看解析收藏纠错

+选题
22. 人们在长期的数学实践中总结了许多解决数学问题的方法，形成了许多光辉的数学思想，其中转化思想是中学数学中最活跃，最实用，也是最重要的数学思想，例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法．
问题提出：求边长分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的三角形的面积．

问题解决：

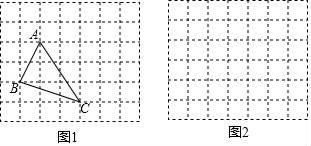
在解答这个问题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出边长分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的格点三角形△ABC（如图1）．AB＝ $\text{[math]}$ 是直角边分别为1和2的直角三角形的斜边，BC＝ $\text{[math]}$ 是直角边分别为1和3的直角三角形的斜边，AC＝ $\text{[math]}$ 是直角边分别为2和3的直角三角形的斜边，用一个大长方形的面积减去三个直角三角形的面积，这样不需求△ABC的高，而借用网格就能计算出它的面积．

（1）请直接写出图1中△ABC的面积为．

（2）类比迁移：求出边长分别为 $\text{[math]}$ 、2 $\text{[math]}$ 、 $\text{[math]}$ 的三角形的面积（请利用图2的正方形网格画出相应的△ABC，并求出它的面积）．

查看解析收藏纠错

+选题
23. 某品牌牛奶供应商提供A，B，C，D四种不同口味的牛奶供学生饮用．某校为了了解学生对不同口味的牛奶的喜好，对全校订牛奶的学生进行了随机调查，并根据调查结果绘制了如下两幅不完整的统计图．
根据统计图的信息解决下列问题：

（1）本次调查的学生有多少人？

（2）补全上面的条形统计图；

（3）扇形统计图中C对应的中心角度数是；

（4）若该校有600名学生订了该品牌的牛奶，每名学生每天只订一盒牛奶，要使学生能喝到自己喜欢的牛奶，则该牛奶供应商送往该校的牛奶中，A，B口味的牛奶共约多少盒？

查看解析收藏纠错

+选题
24. 如图，点P是正方形ABCD内一点，点P到点A、B和D的距离分别为1，2 $\text{[math]}$ ， $\text{[math]}$ ，△ADP沿点A旋转至△ABP′，连结PP′，并延长AP与BC相交于点Q．

（1）求证：△APP′是等腰直角三角形；

（2）求∠BPQ的大小．

查看解析收藏纠错

+选题
25. 潮州旅游文化节开幕前，某凤凰茶叶公司预测今年凤凰茶叶能够畅销，就用32000元购进了一批凤凰茶叶，上市后很快脱销，茶叶公司又用68000元购进第二批凤凰茶叶，所购数量是第一批购进数量的2倍，但每千克凤凰茶叶进价多了10元．

（1）该凤凰茶叶公司两次共购进这种凤凰茶叶多少千克？

（2）如果这两批茶叶每千克的售价相同，且全部售完后总利润率不低于20%，那么每千克售价至少是多少元？

查看解析收藏纠错

+选题
26. 已知，四边形ABCD中，E是对角线AC上一点，DE＝EC，以AE为直径的⊙O与边CD相切于点D，点B在⊙O上，连接OB．

（1）求证：DE＝OE；

（2）若CD∥AB，求证：BC是⊙O的切线；

（3）在（2）的条件下，求证：四边形ABCD是菱形．

查看解析收藏纠错

+选题
27. 已知，抛物线y＝ax²+ax+b(a≠0)与直线y＝2x+m有一个公共点M(1，0)，且a＜b．

（1）求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示)；

（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；

（3） a＝﹣1时，直线y＝﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位(t＞0)，若线段GH与抛物线有两个不同的公共点，试求t的取值范围．

查看解析收藏纠错

+选题

黑龙江省哈尔滨市平房区2019年中考数学二模试卷

一、选择题（满分30分）

二、填空题（满分30分）

三、解答题（满分60分）

相关试卷收起∨

黑龙江省哈尔滨市平房区2019年中考数学二模试卷

一、选择题（满分30分）

二、填空题（满分30分）

三、解答题（满分60分）

相关试卷 收起∨

相关试卷收起∨